题目内容
12. 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
分析 (1)根据矩形的面积公式即可求出S.
(2)利用(1)中的函数关系式,把自变量x的值代入计算即可.
(3)观察(2)中计算结果,即可判断.
解答 解:(1)由题意S=x•$\frac{40-2x}{2}$=-x2+20x.
(2)x=8时,S=96,
x=9时,S=99,
x=9.5时,S=99.75,
x=10时,S=100,
x=10.5时,S=99.75,
x=11时,S=99,
x=12时,S=96.
故答案分别为96,99,99.75,100,99.75,99,96.
(3)猜想:x=10时,S的值最大.
点评 本题考查二次函数的应用,矩形的性质等知识,解题的关键是记住矩形的面积公式,学会构建函数关系式解决实际问题,属于中考常考题型.

练习册系列答案
相关题目
3.若x<0,则|$\sqrt{{x}^{2}}$+3x|=( )
| A. | -4x | B. | 4x | C. | -2x | D. | 2x |
2. 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
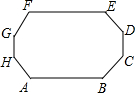 如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.
如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.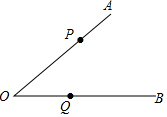 已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图
已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图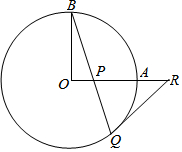 如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.
如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.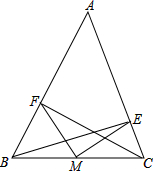 如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.
如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.