题目内容
2.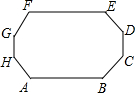 如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.
如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.
分析 双向延长AB、CD、EF、GH得四边形MNPQ,根据多边形内角和定理求出各内角的度数,故可得出其外角的度数,由此得出四边形MNPQ是长方形,BPC、△DQE、△FMG、△ANH都是等腰直角三角形.设GH=x,HA=y,根据MQ=NP可得出y的值,同理得出x的值,进而可得出结论.
解答  解:如图,双向延长AB、CD、EF、GH得四边形MNPQ,
解:如图,双向延长AB、CD、EF、GH得四边形MNPQ,
∵八边形ABCDEFGH的8个内角都相等,
∴每个内角=$\frac{(8-2)×180°}{8}$=135°,
∴每一个外角等于45°,
∴四边形MNPQ是长方形,BPC、△DQE、△FMG、△ANH都是等腰直角三角形.
设GH=x,HA=y,
∵MQ=NP,
∴MF+EF+EQ=NA+AB+BP,即$\sqrt{2}$+6+$\frac{5\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$y+7+2,解得y=3-$\sqrt{2}$.
同理可得,x=3+2$\sqrt{2}$,
∴该八边形的周长=32+$\sqrt{2}$.
点评 本题考查的是三角形的三边关系,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
7.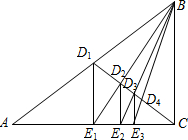 如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
 如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )| A. | $\frac{1}{(n+1)^{2}}$ | B. | $\frac{1}{(2n)^{2}}$ | C. | $\frac{1}{4n}$ | D. | $\frac{1}{{2}^{n+1}}$ |
12. 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
(3)猜一猜,当x为何值时,S的值最大?
 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |

 如图,求图中x的值.
如图,求图中x的值.