题目内容
20．
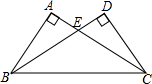如图，∠BAC=90°，∠EDC=90°，∠DCE=30°，ED=2，AB=3，求S△CEB的值．
分析 由含30°角的直角三角形的性质得出CE的长，再根据S△CEB=$\frac{1}{2}$CE•AB，即可得出结果．
解答 解：∵∠BAC=90°，∠EDC=90°，∠DCE=30°，
∴CE=2DE=4，
∴S△CEB=$\frac{1}{2}$CE•AB=$\frac{1}{2}$×4×3=6．
点评 本题考查了含30°角的直角三角形的性质、三角形面积的计算；熟练掌握含30°角的直角三角形的性质，求出CE的长是解决问题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
11．点P（m+6，m-3）在y轴上，则点P的坐标是（ ）
| A． | （-3，0） | B． | （0，3） | C． | （0，-9） | D． | （9，0） |
已知矩形ABCD的周长为20cm．若设AB=xcm，BC=ycm．请写出y与x的函数关系式并写出自变量x的取值范围．
15．
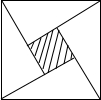2002年8月在北京召开的国际数学家大会会标，它是有四个全等的小正方形拼成的一个大正方形（如图所示），若大正方形的面积为13，小正方形较长的直角边为a，较短的直角边为b，则（a+b）2的值为（ ）
2002年8月在北京召开的国际数学家大会会标，它是有四个全等的小正方形拼成的一个大正方形（如图所示），若大正方形的面积为13，小正方形较长的直角边为a，较短的直角边为b，则（a+b）2的值为（ ）| A． | 13 | B． | 19 | C． | 25 | D． | 169 |
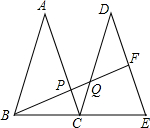如图，△ABC和△DCE是两个全等的等腰三角形，底边BC、CE在一条直线上，F为DE的中点，连接BF，交AC于点P，交DC于点Q，则$\frac{PQ}{PB}$的值等于$\frac{1}{3}$．
12．在直角坐标系中，点M（$\sqrt{3}$，-2）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
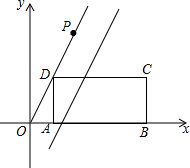如图，在平面直角坐标系中，矩形ABCD的边AB在x轴的正半轴上，点A在点B的左侧，直线y=kx经过点D（1，2）和点P，已知OP=2$\sqrt{5}$，将直线y=kx沿y轴向下平移得到y=kx+b，若点P落在矩形ABCD的内部，那么b的取值范围是（ ）