题目内容
6.不等式$\left\{\begin{array}{l}{\frac{2x-1}{3}-\frac{5x-3}{6}<1,①}\\{|2x-1|≤5,②}\end{array}\right.$的解集是关于x的一元一次不等式ax>-1解集的一部分,求a的取值范围.分析 先求出不等式组解集,再根据解集是关于x的一元一次不等式ax>-1解集的一部分,分a<0和a>0分别求a的范围,综合可得a的取值范围.
解答 解:解不等式①得:x>-5,
解不等式②得:-2≤x≤3,
则不等式组的解集为:-2≤x≤3,
∵不等式组的解集是不等式ax>-1解集的一部分,
∴当a<0时,x<-$\frac{1}{a}$,-$\frac{1}{a}$>3,解得:a<-$\frac{1}{3}$;
当a>0时,x>-$\frac{1}{a}$,-$\frac{1}{a}$<-2,解得:a<$\frac{1}{2}$,
则此时0<a<$\frac{1}{2}$;
综上:a的取值范围是a<-$\frac{1}{3}$或0<a<$\frac{1}{2}$.
点评 本题主要考查解不等式组和解不等式的能力,根据题意分类讨论是前提,根据不等式组解集是一元一次不等式解集的一部分确定a的范围是关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
11.点P(m+6,m-3)在y轴上,则点P的坐标是( )
| A. | (-3,0) | B. | (0,3) | C. | (0,-9) | D. | (9,0) |
 如图,⊙O的直径CD⊥AB,∠A=30°,则∠D=30°.
如图,⊙O的直径CD⊥AB,∠A=30°,则∠D=30°. 如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.
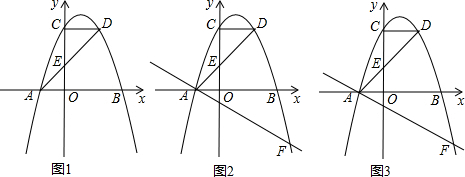
如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.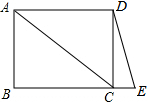 四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.如图,BE=AC,若∠ACB=40°,求∠E的度数.
四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.如图,BE=AC,若∠ACB=40°,求∠E的度数.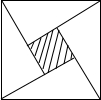 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )