题目内容
10.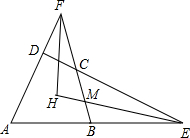 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
分析 连接EF,根据三角形的内角和得到∠CFE+∠CEF+∠FCE=180°,根据已知条件得到∠BAD+∠FCE=180°,由角平分线的性质得到∠CFH=$\frac{1}{2}$∠CFA,∠HEC=$\frac{1}{2}$∠BED,在△AEF中,根据三角形的内角和推出∠CFH+∠BEH+∠CEF+∠FCE=90°,在△HEF中,根据三角形的内角和推出∠CFH+∠BEH+∠CEF+∠FCE+∠H=180°,即可得到结论.
解答 解:连接EF,则∠CFE+∠CEF+∠FCE=180°,
∵∠BAD+∠BCD=180°,∠FCE=∠BCD,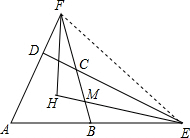
∴∠BAD+∠FCE=180°,
∵∠E,∠F的平分线交于点H,
∴∠CFH=$\frac{1}{2}$∠CFA,∠HEC=$\frac{1}{2}$∠BED,
在△AEF中,
∵∠A+∠CFA+∠CFE+∠CEF+∠BED=180°,
∴∠CFH+∠BEH+∠CEF+∠FCE=90°,
在△HEF中,
∠CFH+∠BEH+∠CEF+∠FCE+∠H=180°,
∴∠H=90°,
∴EH⊥FH.
点评 本题考查了三角形的内角和,多边形的内角和外角,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.满足$-\sqrt{3}<x<\sqrt{7}$的整数共有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.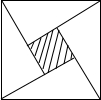 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )| A. | 13 | B. | 19 | C. | 25 | D. | 169 |
19.已知y=x2-x-1,则其图象的开口方向及顶点坐标分别是( )
| A. | 开口向上,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | B. | 开口向下,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | ||
| C. | 开口向上,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) | D. | 开口向下,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) |
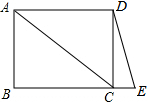 四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.如图,BE=AC,若∠ACB=40°,求∠E的度数.
四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.如图,BE=AC,若∠ACB=40°,求∠E的度数.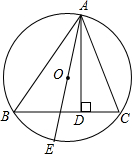 如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证:
如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证: