题目内容
4.计算:(1)$\sqrt{1\frac{15}{49}}$ (2)-$\sqrt{1\frac{2}{3}}$÷$\sqrt{\frac{5}{54}}$ (3)$\sqrt{\frac{0.16×144}{0.64×100}}$ (4)3$\sqrt{20}$÷$\frac{3}{2}$$\sqrt{2\frac{2}{3}}$.
分析 (1)直接将带分数化成假分数,即可开平方得出答案;
(2)直接利用二次根式除法运算法则求出答案;
(3)利用二次根式乘法运算法则化简求出答案;
(4)直接利用二次根式除法运算法则求出答案.
解答 解:(1)$\sqrt{1\frac{15}{49}}$=$\sqrt{\frac{64}{49}}$=$\frac{8}{7}$;
(2)-$\sqrt{1\frac{2}{3}}$÷$\sqrt{\frac{5}{54}}$=-$\sqrt{\frac{5}{3}×\frac{54}{5}}$=-3$\sqrt{2}$;
(3)$\sqrt{\frac{0.16×144}{0.64×100}}$=$\sqrt{\frac{144}{100}}$×$\sqrt{\frac{0.16}{0.64}}$
=$\frac{6}{5}$×$\frac{1}{2}$
=$\frac{3}{5}$;
(4)3$\sqrt{20}$÷$\frac{3}{2}$$\sqrt{2\frac{2}{3}}$
=3×$\frac{2}{3}$×$\sqrt{20×\frac{3}{8}}$
=2$\sqrt{\frac{15}{2}}$
=$\sqrt{30}$.
点评 此题主要考查了二次根式的乘除运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
15.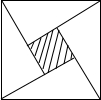 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )| A. | 13 | B. | 19 | C. | 25 | D. | 169 |
12.在直角坐标系中,点M($\sqrt{3}$,-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.已知y=x2-x-1,则其图象的开口方向及顶点坐标分别是( )
| A. | 开口向上,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | B. | 开口向下,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | ||
| C. | 开口向上,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) | D. | 开口向下,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) |
 如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.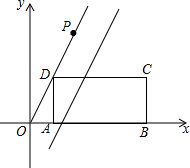 如图,在平面直角坐标系中,矩形ABCD的边AB在x轴的正半轴上,点A在点B的左侧,直线y=kx经过点D(1,2)和点P,已知OP=2$\sqrt{5}$,将直线y=kx沿y轴向下平移得到y=kx+b,若点P落在矩形ABCD的内部,那么b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边AB在x轴的正半轴上,点A在点B的左侧,直线y=kx经过点D(1,2)和点P,已知OP=2$\sqrt{5}$,将直线y=kx沿y轴向下平移得到y=kx+b,若点P落在矩形ABCD的内部,那么b的取值范围是( )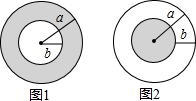 如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )
如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )