题目内容
20．
如图，在△ABC中，点D、E分别是AC、BC边上的点，且DE∥AB，CD：AD=2：1，DE=6，则AB的长为9．
分析 根据相似三角形的判定和性质得到比例式，代入数据即可得到结论．
解答 解：∵CD：AD=2：1，
∴CD：AC=2：3，
∵DE∥AB，
∴△CDE∽△CAB，
∴$\frac{CD}{CA}=\frac{DE}{AB}$，
即$\frac{6}{AB}=\frac{2}{3}$，
∴AB=9．
故答案为：9．
点评 此题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
如图，某小区规划在一个长为16m、宽为9m的矩形场地ABCD上修建三条同样宽的小路，使其中两条与AB平行，另一条与AD平行，其余部分种草．若草坪部分的总面积为112m2，求小路的宽度．若设小路的宽度为xm，则x满足的方程为（16-2x）（9-x）=112．
2．
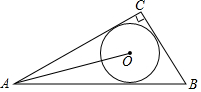如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，⊙O是△ABC的内切圆，连接OA，则sin∠OAB的值为（ ）
如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，⊙O是△ABC的内切圆，连接OA，则sin∠OAB的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{\sqrt{10}}{10}$ | D． | $\frac{\sqrt{2}}{4}$ |
如图，已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点，P是以C（0，2）为圆心，2为半径的圆上一动点，连结PA、PB．则△PAB面积的最大值是13．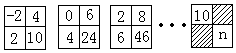
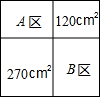小区内有一块正方形空地，物业计划利用这块空地修建居民休闲区，具体规划如图所示，其中A，B为活动区域，剩余两个正方形区域为绿化区域，面积分别是270m2和120m2，则A，B两个活动区域的总面积为360m2．