题目内容
1. 如图,在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,∠DCB=120°,连接对角线BD,则△ABD的面积为$\frac{\sqrt{11}}{4}$.
如图,在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,∠DCB=120°,连接对角线BD,则△ABD的面积为$\frac{\sqrt{11}}{4}$.
分析 过点C作CE⊥BD,由已知条件可求出DE的长,则BD的长也可求出,再利用等腰三角形的性质可求出进而可求出△ABD的面积.
解答 解:过点C作CE⊥BD,
∵BC=CD=1,∠DCB=120°,
∴∠DCE=60°,DE=BE,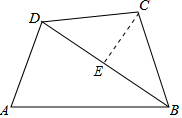
∴∠CDE=30°,
∴CE=$\frac{1}{2}$DC=$\frac{1}{2}$,
∴DE=$\frac{\sqrt{3}}{2}$,
∴BD=$\sqrt{3}$,
∵AB=$\sqrt{3}$,
∴AB=BD,
∵AD=1,
∴AD边上的高=$\sqrt{3-\frac{1}{4}}$=$\frac{\sqrt{11}}{2}$,
∴△ABD的面积=$\frac{1}{2}$AD•$\frac{\sqrt{11}}{2}$=$\frac{\sqrt{11}}{4}$,
故答案为:$\frac{\sqrt{11}}{4}$.
点评 本题考查了解直角三角形的有关知识,用到的其他知识点还有勾股定理的运用、三角形面积公式的运用以及特殊角的锐角三角函数值、等腰三角形的性质,作出△DCB的高线CE是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
2.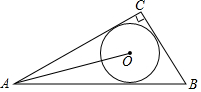 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{\sqrt{2}}{4}$ |
16.方程x+2y=5的非负整数解有( )
| A. | 无数个 | B. | 3个 | C. | 4个 | D. | 5个 |
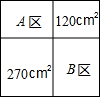 小区内有一块正方形空地,物业计划利用这块空地修建居民休闲区,具体规划如图所示,其中A,B为活动区域,剩余两个正方形区域为绿化区域,面积分别是270m2和120m2,则A,B两个活动区域的总面积为360m2.
小区内有一块正方形空地,物业计划利用这块空地修建居民休闲区,具体规划如图所示,其中A,B为活动区域,剩余两个正方形区域为绿化区域,面积分别是270m2和120m2,则A,B两个活动区域的总面积为360m2.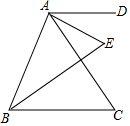 已知,如图,AD∥BC,AE、BE分别平分∠DAC和∠ABC.若∠DAC=50°,∠ABC=70°,则∠E的度数是60°.
已知,如图,AD∥BC,AE、BE分别平分∠DAC和∠ABC.若∠DAC=50°,∠ABC=70°,则∠E的度数是60°.