题目内容
已知C点是长为18cm的线段AB上的一点,根据下列条件,求AC、BC的长.
(1)AC是BC的2倍;
(2)AC:BC=3:2;
(3)AC比BC长4cm.
(1)AC是BC的2倍;
(2)AC:BC=3:2;
(3)AC比BC长4cm.
考点:两点间的距离
专题:
分析:(1)根据线段的和差,可得方程,根据解方程,可得答案;
(2)根据线段的和差,可得方程,根据解方程,可得答案;
(3)根据线段的和差,可得方程,根据解方程,可得答案.
(2)根据线段的和差,可得方程,根据解方程,可得答案;
(3)根据线段的和差,可得方程,根据解方程,可得答案.
解答:解:(1)设BC的长是xcm,那么AC的长是2xcm,由线段的和差,得
x+2x=18,
解得x=6,2x=12,
即AC=12(cm),BC=6(cm);
(2)设AC=3xcm,BC=2xcm,由线段的和差,得
3x+2x=18.
解得x=3.6,
3x=10.8,
2x=7.2,
即AC=10.8(cm),BC=7.2(cm);
(3)设BC的长是xcm,AC的长是(x+4)cm,由线段的和差,得
x+(x+4)=18.
解得x=7,
x+4=11,
即BC的长是7cm,AC的长是11cm.
x+2x=18,
解得x=6,2x=12,
即AC=12(cm),BC=6(cm);
(2)设AC=3xcm,BC=2xcm,由线段的和差,得
3x+2x=18.
解得x=3.6,
3x=10.8,
2x=7.2,
即AC=10.8(cm),BC=7.2(cm);
(3)设BC的长是xcm,AC的长是(x+4)cm,由线段的和差,得
x+(x+4)=18.
解得x=7,
x+4=11,
即BC的长是7cm,AC的长是11cm.
点评:本题考查了两点间的距离,利用线段的和差列方程是解题关键.

练习册系列答案
相关题目
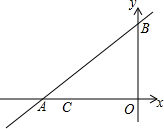 如图,直线y=
如图,直线y=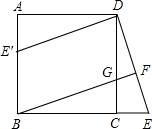 如图所示,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接
如图所示,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接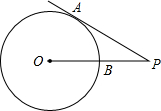 如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为
如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为