题目内容
如图1,边长为6的等边△ABC中,点D沿射线AB方向由A向B运动,点F同时从C出发,以相同的速度沿射线BC方向运动,过点D作DE⊥AC,连结DF交射线AC于点G.
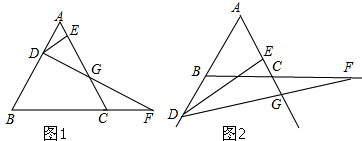
(1)当点D运动到AB的中点时,求AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图2的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,请证明EG等于AC的一半.

(1)当点D运动到AB的中点时,求AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图2的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,请证明EG等于AC的一半.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)解直角三角形ADE,根据30°角对应直角边为斜边长一半即可解题;
(2)设AD=X,解直角三角形BDF即可求得X的值,即可求得△BDF的面积;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
(2)设AD=X,解直角三角形BDF即可求得X的值,即可求得△BDF的面积;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
解答:解:(1)当D为AB中点时,AD=3,
在RT△ADE中,∠A=60°,∠ADE=30°,
∴AE=AD•sinA=
.
(2)设AD=X,则CF=X,
当DF⊥AB时,RT△BDF中,∠F=30°,
∴BF=2BD,6+X=2(6-X),
解得X=2,∴AD=2.
∴BD=6-2=4,
DF=BD•tanB=4
.
∴△BDF的面积为
BD•DF=8
.
(3)过F作FH⊥AC,
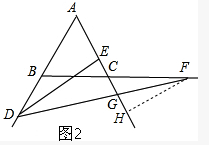
在△ADE和△CFH中,
,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
,
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=
EH=
AC.
在RT△ADE中,∠A=60°,∠ADE=30°,
∴AE=AD•sinA=
| 3 |
| 2 |
(2)设AD=X,则CF=X,
当DF⊥AB时,RT△BDF中,∠F=30°,
∴BF=2BD,6+X=2(6-X),
解得X=2,∴AD=2.
∴BD=6-2=4,
DF=BD•tanB=4
| 3 |
∴△BDF的面积为
| 1 |
| 2 |
| 3 |
(3)过F作FH⊥AC,

在△ADE和△CFH中,
|
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
|
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证GDE≌△GFH是解题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆的斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆的斜边AB交于点E,连接DE.