题目内容
 如图所示,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接
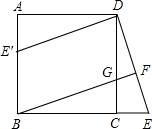
如图所示,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F,将△DCE绕点D顺时针旋转90°得到△DAE′.
(1)判断四边形E′BGD是什么特殊四边形,并说明理由.
(2)由△BCG经过怎样的变换可得到△DAE′?请说出具体的变换过程.
考点:旋转的性质
专题:
分析:(1)由四边形ABCD是矩形,可得AB∥CD,AB=CD,由旋转的性质知AE′=CE=CG,所以BE′=DG,从而证得四边形E′BGD为平行四边形;
(2)首先易证的△BCG≌△DCE(SAS),可得由△BCG绕点C顺时针旋转90°可得到△DCE,再绕点D顺时针旋转90°得到△DAE′.
(2)首先易证的△BCG≌△DCE(SAS),可得由△BCG绕点C顺时针旋转90°可得到△DCE,再绕点D顺时针旋转90°得到△DAE′.
解答:解:(1)四边形E′BGD是平行四边形.
理由:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∵将△DCE绕点D顺时针旋转90°得到△DAE′,
∴CE=AE′,
∵CE=CG,
∴AE′=CG,
∴BE=DG,
∴四边形E′BGD是平行四边形;
(2)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
在△BCG和△DCE,
∴△BCG≌△DCE(SAS);
∴由△BCG绕点C顺时针旋转90°可得到△DCE,再绕点D顺时针旋转90°得到△DAE′.
理由:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∵将△DCE绕点D顺时针旋转90°得到△DAE′,
∴CE=AE′,
∵CE=CG,
∴AE′=CG,
∴BE=DG,
∴四边形E′BGD是平行四边形;
(2)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
在△BCG和△DCE,
|
∴△BCG≌△DCE(SAS);
∴由△BCG绕点C顺时针旋转90°可得到△DCE,再绕点D顺时针旋转90°得到△DAE′.
点评:此题考查了旋转的性质、全等三角形的判定与性质以及平行四边形的判定.此题难度适中,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知在正方形的网格中,网线的交点称为格点,如图,点A、B、C都是格点.每个小正方形的边长为1个单位长度,若在网格中建立坐标系,则A的坐标为(-1,3),B的坐标为(1,3),C的坐标为(3,1).
已知在正方形的网格中,网线的交点称为格点,如图,点A、B、C都是格点.每个小正方形的边长为1个单位长度,若在网格中建立坐标系,则A的坐标为(-1,3),B的坐标为(1,3),C的坐标为(3,1).