题目内容
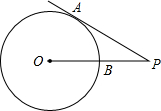 如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为
如图,点P为⊙O外一点,PA切⊙O于A,PO交⊙O于B,若PA交⊙O于B,若PA=3,PB=1,则⊙O半径为考点:切线的性质
专题:计算题
分析:连接OA,如图,设⊙O的半径为r,根据切线的性质,由PA切⊙O于A得到OA⊥PA,然后在Rt△PAO利用勾股定理得r2+32=(r+1)2,然后解方程即可.
解答:解:连接OA,如图, 设⊙O的半径为r,
设⊙O的半径为r,
∵PA切⊙O于A,
∴OA⊥PA,
∴∠PAO=90°,
在Rt△PAO,OA=r,OP=OB+PB=r+1,PA=3,
∵OA2+PA2=OP2,
∴r2+32=(r+1)2,解得r=4,
即⊙O的半径为4.
 设⊙O的半径为r,
设⊙O的半径为r,∵PA切⊙O于A,
∴OA⊥PA,
∴∠PAO=90°,
在Rt△PAO,OA=r,OP=OB+PB=r+1,PA=3,
∵OA2+PA2=OP2,
∴r2+32=(r+1)2,解得r=4,
即⊙O的半径为4.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 已知在正方形的网格中,网线的交点称为格点,如图,点A、B、C都是格点.每个小正方形的边长为1个单位长度,若在网格中建立坐标系,则A的坐标为(-1,3),B的坐标为(1,3),C的坐标为(3,1).
已知在正方形的网格中,网线的交点称为格点,如图,点A、B、C都是格点.每个小正方形的边长为1个单位长度,若在网格中建立坐标系,则A的坐标为(-1,3),B的坐标为(1,3),C的坐标为(3,1). 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,DC=4,BC=6,点E在射线BA上,若△EBC是以EB为腰的等腰三角形,则∠ECB的正切值
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,DC=4,BC=6,点E在射线BA上,若△EBC是以EB为腰的等腰三角形,则∠ECB的正切值 如图,AB、CD为⊙O的直径,
如图,AB、CD为⊙O的直径,