题目内容
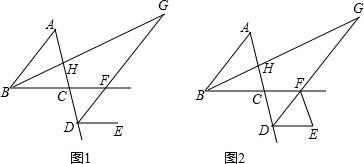
12.如图,在△ABC中,点D是AC延长线上的一点,过点D作DE∥BC,DG平分∠ADE,BG平分∠ABC,DG与BG交于点G.(1)如图1,若∠A=50°.求∠G的度数;
(2)如图2,连接FE,若∠DFE=$\frac{1}{2}$∠ABC+∠G.求证:FE∥AD.
分析 (1)在图中添上点M,由DE∥BC结合外角的性质可得出∠ADE=∠A+∠ABC,再根据角平分线的性质可得出∠GDE=$\frac{1}{2}$(∠A+∠ABC),由此可得出∠GFM=$\frac{1}{2}$(∠A+∠ABC)=∠GBF+∠G,从而得出∠G=$\frac{1}{2}$∠A,根据∠A的度数即可得出结论;
(2)由(1)可得知:∠CDF=∠GDE=$\frac{1}{2}$(∠A+∠ABC),∠G=$\frac{1}{2}$∠A,再结合已知∠DFE=$\frac{1}{2}$∠ABC+∠G,即可得出∠DFE=∠CDF,根据平行线的判定定理“内错角相等,两直线平行”即可证出FE∥AD.
解答 (1)解:在BF延长线上标上点M,如图所示.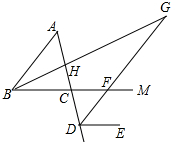
∵DE∥BC,
∴∠ADE=∠ACF=∠A+∠ABC,∠GFM=∠GDE.
∵DG平分∠ADE,BG平分∠ABC,
∴∠GDE=$\frac{1}{2}$∠ACF=$\frac{1}{2}$(∠A+∠ABC),∠GBF=$\frac{1}{2}$∠ABC,
∴∠GFM=$\frac{1}{2}$(∠A+∠ABC)=∠GBF+∠G,
∴∠G=$\frac{1}{2}$∠A=25°.
(2)证明:由(1)知:∠CDF=∠GDE=$\frac{1}{2}$(∠A+∠ABC),∠G=$\frac{1}{2}$∠A,
∵∠DFE=$\frac{1}{2}$∠ABC+∠G=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠A=$\frac{1}{2}$(∠A+∠ABC)=∠CDF,
∴FE∥AD.
点评 本题考查了平行线的判定及性质、角平分线的性质以及三角形外角的性质,解题的关键是:(1)求出∠G=$\frac{1}{2}$∠A;(2)通过角的计算找出∠DFE=∠CDF.本题属于基础题,难度不大,解决该题型题目时,利用平行线的性质找出相等(或互补)的角是关键.

 了了解九年级男生的立定跳远成绩,体育老师对该校九年级的260位男生进行了一次立定跳远测试.已知,九年级男生立定跳远成绩(x)的达标要求是:x<185为不合格;185≤x<225为合格;x≥225为优秀(单位:cm).随机以40位男为生的测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
了了解九年级男生的立定跳远成绩,体育老师对该校九年级的260位男生进行了一次立定跳远测试.已知,九年级男生立定跳远成绩(x)的达标要求是:x<185为不合格;185≤x<225为合格;x≥225为优秀(单位:cm).随机以40位男为生的测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:| 组别 | 成绩x(cm) | 频数(人数) |
| 第1组 | 165≤x<185 | 4 |
| 第2组 | 185≤x<205 | 6 |
| 第3组 | 205≤x<225 | |
| 第4组 | 225≤x<245 | 18 |
| 第5组 | 245≤x<265 | 4 |
(1)请把频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第几组?
(3)估计该校九年级男生立定跳远成绩为优秀的有多少人?
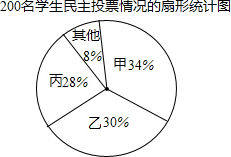 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:| 试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
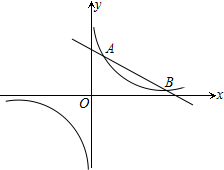 如图,双曲线$y=\frac{k}{x}$(k>0)与直线$y=-\frac{1}{2}x+4$相交于A、B两点
如图,双曲线$y=\frac{k}{x}$(k>0)与直线$y=-\frac{1}{2}x+4$相交于A、B两点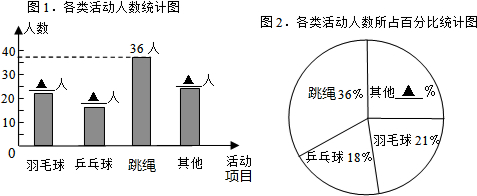
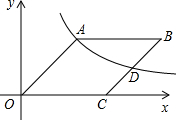 如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.
如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.