题目内容
9.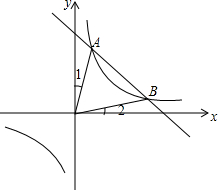 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).(1)当k1的值;
(2)当x<1时,观察图象,比较y1与y2的大小;
(3)分别连接OA,OB,当∠1=∠2时,求y2关于x的函数表达式.
分析 (1)把A点坐标代入反比例函数解析式,即可求出k1的值;
(2)根据图象和A的坐标即可得出答案;
(3)作AC⊥y轴于C,BD⊥x轴于D,根据题意求得B的坐标为(4,1),然后把A、B的坐标代入y2=k2x+b,根据待定系数法即可求得解析式.
解答 解:(1)∵函数y1=$\frac{{k}_{1}}{x}$的图象过A(1,4),
∴将A点坐标代入函数解析式得:4=$\frac{{k}_{1}}{1}$,
解得k1=4;
(2)当0<x<1时,双曲线在直线的上方,即y1>y2;
当x<0时,双曲线在直线的下方,即y1<y2;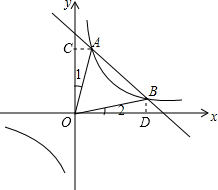 (3)作AC⊥y轴于C,BD⊥x轴于D,
(3)作AC⊥y轴于C,BD⊥x轴于D,
∵函数y1=$\frac{4}{x}$的图象经过A,B两点,
∴S△OAC=S△BOD=$\frac{1}{2}$×4=2,
∵∠OCA=∠ODB=90°,∠1=∠2,
∴△OAC∽△OBD,
∴$\frac{OC}{OD}$=$\frac{AC}{BD}$=1,
∴B(4,1),
把A(1,4)、B(4,1)代入y2=k2x+b得
$\left\{\begin{array}{l}{{k}_{2}+b=4}\\{4{k}_{2}+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=-1}\\{b=5}\end{array}\right.$,
∴y2关于x的函数表达式为y2=-x+5.
点评 本题考查了反比例函数图象与一次函数图象的交点问题以及反比例函数比例系数k的几何意义,主要利用了待定系数法求函数解析式.

练习册系列答案
相关题目
20. 如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
 如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )| A. | 10尺 | B. | 11尺 | C. | 12尺 | D. | 13尺 |
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( ) 如图,在下面的网络图中,按要求画出图形,并回答问题:
如图,在下面的网络图中,按要求画出图形,并回答问题: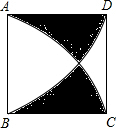 已知,如图,正方形ABCD是边长为1的正方形,分别以A、B为圆心,1为半径画弧,求阴影部分面积.
已知,如图,正方形ABCD是边长为1的正方形,分别以A、B为圆心,1为半径画弧,求阴影部分面积. 已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右作正方形CDEF,连结BF.若S△OBC=8,AC=BC.
已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右作正方形CDEF,连结BF.若S△OBC=8,AC=BC.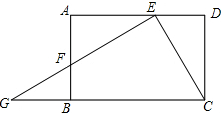 如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC交边AB于点F,交CB的延长线于点G,且EF=EC.
如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC交边AB于点F,交CB的延长线于点G,且EF=EC.