题目内容
17. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )①$\frac{CF}{DF}$=$\frac{1}{3}$;②AE2=AD•AF;③△ADF≌△ABE;④图中有3对相似三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由题中条件可得△CEF∽△BAE,进而得出对应线段成比例,进而又可得出△ABE∽△AEF,即可得出题中结论.
解答 解:∵四边形ABCD 是正方形,
∴∠B=90°,
∵AE⊥EF,
∴∠BAE+∠AEB=∠FEC+∠AEB=90°,
∴∠BAE=∠CEF,
∴△CEF∽△BAE,
∴$\frac{CE}{AB}$=$\frac{CF}{BE}$,
∵E是BC的中点,
∴$\frac{CF}{CE}$=$\frac{1}{2}$,
∴$\frac{CF}{DF}$$\frac{1}{3}$,故①正确;
由△CEF∽△BAE可得$\frac{CE}{CF}$=$\frac{AB}{BE}$,
∴∠EAF=∠BAE的正切值相同,
∴∠EAF=∠BAE,
∵∠B=∠C=90°,
∴△ABE∽△AEF,
∴$\frac{AB}{AE}$=$\frac{AE}{AF}$,
∴AE2=AB•AF,
∵AD=AB,
∴AE2=AD•AF,故②正确;
∵$\frac{AB}{BE}$=2,$\frac{AD}{DF}$=$\frac{4}{3}$,
∴$\frac{AB}{BE}$$≠\frac{AD}{DF}$,
∴△ADF与△ABE不全等,故③错误;
由以上证得△CEF∽△BAE,△ABE∽△AEF,
∴△CEF∽△AEF,故④正确.
故选C.
点评 本题主要考查了相似三角形的判定及性质,其中又涉及正方形的一些性质问题,能够熟练掌握这些定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
①起跑后1小时内,甲在乙的前面; ②第1小时两人都跑了10千米;
③甲比乙先到达终点; ④两人都跑了20千米.
正确的有( )
 在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:①起跑后1小时内,甲在乙的前面; ②第1小时两人都跑了10千米;
③甲比乙先到达终点; ④两人都跑了20千米.
正确的有( )
| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
12. 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )| A. | 6m2 | B. | 21m2 | C. | 3m2 | D. | 5m2 |
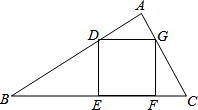 如图,正方形DEFG内接于△ABC,且△ADG、△BDE、△CFG的面积分别为1、3、1,则正方形DEFG的面积是4.
如图,正方形DEFG内接于△ABC,且△ADG、△BDE、△CFG的面积分别为1、3、1,则正方形DEFG的面积是4. 如图,有一张长为5,宽为1的矩形纸片,要通过适当的剪拼,得到一个与之面积相等的正方形
如图,有一张长为5,宽为1的矩形纸片,要通过适当的剪拼,得到一个与之面积相等的正方形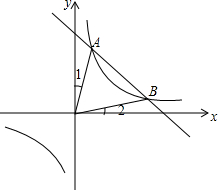 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).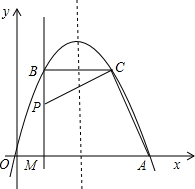 如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.