题目内容
20.在△ABC中,AB=$4\sqrt{3}$,∠ABC=30°,BC=10,点P在直线AC上,点P到直线AB的距离为1,则CP的长为$\frac{8\sqrt{7}}{5}$或$\frac{12\sqrt{7}}{5}$.分析 过点C作CD⊥AB交BA的延长线于点D,根据∠ABC的正弦和余弦可以求出CD、BD的长度,从而可以求出AD的长度,然后利用勾股定理即可求出AC的长度,再利用相似三角形对应边成比例列式求出AP的长度,再分点P在线段AC上与点P在射线CA上两种情况讨论求解.
解答 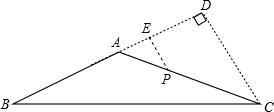 解:如图,过点C作CD⊥AB交BA的延长线于点D,
解:如图,过点C作CD⊥AB交BA的延长线于点D,
∵BC=10,∠ABC=30°,
∴CD=BCsin30°=5,
BD=BCcos30°=5$\sqrt{3}$,
∵AB=4$\sqrt{3}$,
∴AD=BD-AB=5$\sqrt{3}$-4$\sqrt{3}$=$\sqrt{3}$,
在Rt△ACD中,AC=$\sqrt{{CD}^{2}{+AD}^{2}}$=2$\sqrt{7}$,
过P作PE⊥AB,与BA的延长线于点E,
∵点P在直线AC上,点P到直线AB的距离为1,
∴△APE∽△ACD,
∴$\frac{AP}{AC}$=$\frac{PE}{CD}$,
即$\frac{AP}{2\sqrt{7}}$=$\frac{1}{5}$,
解得AP=$\frac{2\sqrt{7}}{5}$,
∴①点P在线段AC上时,CP=AC-AP=2$\sqrt{7}$-$\frac{2\sqrt{7}}{5}$=$\frac{8\sqrt{7}}{5}$,
②点P在射线CA上时,CP=AC+AP=2$\sqrt{7}$+$\frac{2\sqrt{7}}{5}$=$\frac{12\sqrt{7}}{5}$,
综上所述,CP的长为$\frac{8\sqrt{7}}{5}$或$\frac{12\sqrt{7}}{5}$.
故答案为:$\frac{8\sqrt{7}}{5}$或$\frac{12\sqrt{7}}{5}$.
点评 本题考查了解直角三角形,作出图形,利用好30°的角构造出直角三角形是解题的关键,要注意分情况讨论,避免漏解.

 在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:①起跑后1小时内,甲在乙的前面; ②第1小时两人都跑了10千米;
③甲比乙先到达终点; ④两人都跑了20千米.
正确的有( )
| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )| A. | 6m2 | B. | 21m2 | C. | 3m2 | D. | 5m2 |
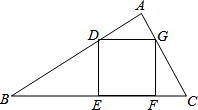 如图,正方形DEFG内接于△ABC,且△ADG、△BDE、△CFG的面积分别为1、3、1,则正方形DEFG的面积是4.
如图,正方形DEFG内接于△ABC,且△ADG、△BDE、△CFG的面积分别为1、3、1,则正方形DEFG的面积是4.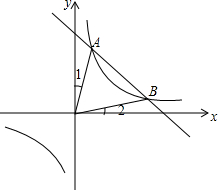 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).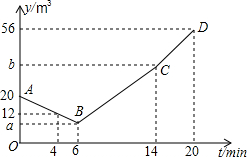 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.