题目内容
14.对于一元二次方程ax2+bx+c=0(a≠0),有下列四种条件:①b2-4ac>0;②b2+4ac>0(a≠0)③a、c异号;④a+b+c的值为零.满足其中之一的方程一定有实数根的有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
分析 由b2-4ac>0,得出一元二次方程ax2+bx+c=0有两个不相等的实数根,①正确;由根的判别式得出②不正确;由a、c异号,得出△=b2-4ac>0,③正确;若a+b+c=0,b=-(a+c),得出△=b2-4ac=(a-c)2≥0,④正确;即可得出结论.
解答 解:∵b2-4ac>0,
∴一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,
∴①正确;
若b2+4ac>0(a≠0),一元二次方程ax2+bx+c=0(a≠0)的根不能确定,
∴②不正确;
∵a、c异号,则△=b2-4ac>0,
∴一元二次方程ax2+bx+c=0一定有实数根,
∴③正确;
∵a+b+c=0,
∴b=-(a+c),
∴△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,
∴一元二次方程ax2+bx+c=0有两个实数根,
∴④正确;
故选:C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
4.如图,有四个大小相同的小长方形和两个大小相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是( )
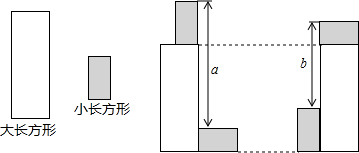

| A. | 3b-2a | B. | $\frac{a-b}{2}$ | C. | $\frac{a-b}{3}$ | D. | $\frac{a}{3}-\frac{b}{4}$ |
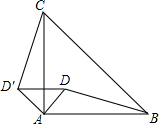 如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置,则∠ADD′=45°.
如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置,则∠ADD′=45°.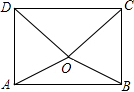 如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长2$\sqrt{7}$d.
如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长2$\sqrt{7}$d.