题目内容
2.已知x=$\frac{\sqrt{8}-\sqrt{7}}{\sqrt{8}+\sqrt{7}}$,y=$\frac{\sqrt{8}+\sqrt{7}}{\sqrt{8}-\sqrt{7}}$,求$\frac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}$的值.分析 化简x、y的值,代入化简后的代数式即可求得.
解答 解:∵x=$\frac{\sqrt{8}-\sqrt{7}}{\sqrt{8}+\sqrt{7}}$,y=$\frac{\sqrt{8}+\sqrt{7}}{\sqrt{8}-\sqrt{7}}$,
化简得x=($\sqrt{8}$-$\sqrt{7}$)2,y=($\sqrt{8}$+$\sqrt{7}$)2,
∵$\frac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})^{2}}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$+$\sqrt{y}$,
∴原式=$\sqrt{8}$-$\sqrt{7}$+$\sqrt{8}$+$\sqrt{7}$=4$\sqrt{2}$.
点评 本题考查了二次根式的化简,利用平方差公式化简是去掉分母中的根号的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
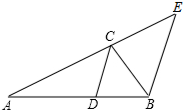 如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.
如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.