题目内容
9.已知一次函数y=(m+3)x+(2-n).(1)m为何值时,y随x的增大而减小?
(2)m,n为何值时,函数图象与y轴的交点在y轴的正半轴?
(3)m,n为何值时,函数图象过二、三、四象限?
(4)m,n为何值时,函数图象过原点?
(5)m,n为何值时,函数图象不经过第一象限?
分析 (1)当m+3<0,y随x的增大而减小;
(2)当m+3≠0,2-n>0,函数图象与y轴的交点在y轴的正半轴;
(3)当m+3<0,2-n<0,函数图象过二、三、四象限.
(4)当m+3≠0,2-n=0,函数图象经过原点;
(5)当m+3<0,2-n≤0,函数图象不经过第一象限.
解答 解:(1)当m+3<0,即m<-3,y随x的增大而减小,
所以当m<-2,n为任何实数,y随x的增大而减小;
(2)当m+3≠0,2-n>0,函数图象与y轴的交点在y轴的正半轴,
解不等式得,m≠-3,n<2,
所以当m≠-3,n<2时,函数图象与y轴的交点在y轴的正半轴;
(3)当m+3<0,2-n<0,函数图象过二、三、四象限,
解不等式得,m<-3,n>2,
所以当m<-3,n>2时,函数图象过二、三、四象限;
(4)当m+3≠0,2-n=0,函数图象经过原点,
解不等式、方程得,m≠-3,n=2,
所以当m≠-3,n=2时,函数图象经过原点.
(5)当m+3<0,2-n≤0,函数图象不经过第一象限,
解不等式得,m<-3,n≥2,
所以当m<-3,n≥2时,函数图象不经过第一象限.
点评 本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.它的图象为一条直线,当k>0,图象经过第一,三象限,y随x的增大而增大;当k<0,图象经过第二,四象限,y随x的增大而减小;当b>0,图象与y轴的交点在x轴的上方;当b=0,图象过坐标原点;当b<0,图象与y轴的交点在x轴的下方.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
20.已知∠α=45°,那么∠α的补角为( )
| A. | 55° | B. | 45° | C. | 145° | D. | 135° |
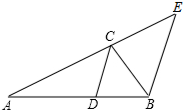 如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.
如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.
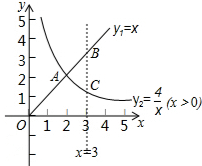 如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:
如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论: