题目内容
6.口袋中有15个球,其中白球有x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球则获胜;甲将摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.(1)当x为何值时,乙获胜的可能性比甲大?
(2)则当x为何值时,游戏对双方公平?
分析 (1)根据题意表示出甲和乙分别获胜的概率,由题意得出不等式,解不等式即可;
(2)令两概率相等得出方程,解方程即可求出x的值.
解答 解:(1)根据题意得:甲获胜的概率=$\frac{2x}{15}$,乙获胜的概率=$\frac{15-x-2x}{15}$,
若乙获胜的可能性比甲大,则$\frac{2x}{15}$<$\frac{15-x-2x}{15}$,
解得:x<3,
即0<x<3(x为正整数)时,乙获胜的可能性比甲大;
(2)根据题意得:$\frac{2x}{15}$=$\frac{15-x-2x}{15}$,
解得:x=3,
即x=3时,两概率相等,游戏对双方公平.
点评 此题考查了游戏的公平性、概率的求法;判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
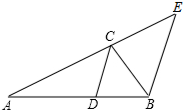 如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.
如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.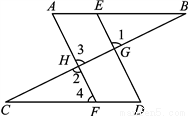

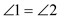 ,(3)BE∥CF任选两个作为条件,另一个作为结论,编一道数学题,并说明理由。
,(3)BE∥CF任选两个作为条件,另一个作为结论,编一道数学题,并说明理由。