题目内容
15.在平面直角坐标系中有一个等腰三角形ABC,点A的坐标为(0,0),点B的坐标为(8,0),底边AB上的高为3,则点C的坐标为(4,3).分析 根据已知条件得到AB=8,根据等腰三角形的性质得到AD=$\frac{1}{2}$AB=4,于是得到结论.
解答  解:如图,
解:如图,
∵点A的坐标为(0,0),点B的坐标为(8,0),
∴AB=8,
∵AC=BC,CD⊥AB,
∴AD=$\frac{1}{2}$AB=4,
∵CD=3,
∴C(4,3),
故答案为:(4,3).
点评 本题考查了等腰三角形的性质,坐标与图形的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
6.已知a,b,c是三角形的三条边,则|a+b-c|-|c-a-b|的化简结果为( )
| A. | 0 | B. | 2a+2b | C. | 2c | D. | 2a+2b-2c |
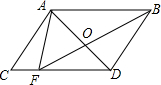 如图,平行四边形ABDC的面积为112平方厘米,又知AB=4CF,求三角形AOF的面积.
如图,平行四边形ABDC的面积为112平方厘米,又知AB=4CF,求三角形AOF的面积.
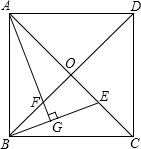 如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.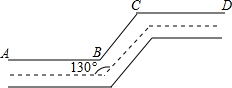 如图,一条公路两次转完后又回到原来的方向(即AB∥CD),如果第一次转弯时的∠B=130°,那么第二次转弯时的∠C=130度.
如图,一条公路两次转完后又回到原来的方向(即AB∥CD),如果第一次转弯时的∠B=130°,那么第二次转弯时的∠C=130度.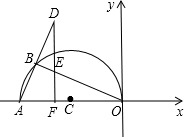 在平面直角坐标系中,点A(-5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=$\frac{3}{2}$或6.
在平面直角坐标系中,点A(-5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=$\frac{3}{2}$或6.