Question

7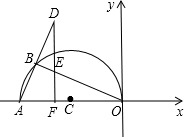．在平面直角坐标系中，点A（-5，0），以OA为直径在第二象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，作点A关于点B的对称点D，过点D作x轴垂线，分别交直线OB、x轴于点E、F，点F为垂足，当DF=4时，线段EF=$\frac{3}{2}$或6．

Answer 1

分析 分点D在第一、二象限．连接OD，则OD=OA=5，在直角三角形ODF中，可求出OF的长度，从而找出AF的长度，在直角三角形ADF中由勾股定理求出AD及DB的长度，由相似三角形的判定定理找出△DBE∽△DFA，结合三角形相似的性质找出$\frac{DE}{DA}=\frac{DB}{DF}$，套用DE=$\frac{DB•DA}{DF}$得出DE值，再由EF=|DF-DE|得出结论．

解答 解：①当点D在第二象限时，连接OD，
∵点A、点D关于B点对称，
∴OD=OA=5．
在Rt△ODF中，OD=5，DF=4，∠DFO=90°，
∴OF=$\sqrt{O{D}^{2}-D{F}^{2}}$=3，
∴AF=OA-OF=2．
∵AO为⊙C的直径，
∴∠ABO=90°，
∴∠DBE=90°=∠DFA，
又∵∠BDE=∠FDA，
∴△BDE∽△FDA，
∴$\frac{DE}{DA}=\frac{DB}{DF}$．
在Rt△ADF中，AF=2，DF=4，∠AFD=90°，
∴AD=$\sqrt{D{F}^{2}+A{F}^{2}}$=2$\sqrt{5}$．
∵OA=OD，且OB⊥AD，
∴AB=DB=$\frac{1}{2}$AD=$\sqrt{5}$，
∴DE=$\frac{DB•DA}{DF}$=$\frac{5}{2}$，
∴EF=DF-DE=$\frac{3}{2}$；
②当点D在第一象限时，连接OD，
∵AO为直径，
∴∠ABO=90°=∠DBO．
在△ABO和△DBO中，$\left\{\begin{array}{l}{AB=DB}\\{∠ABO=∠DBO}\\{OB=OB}\end{array}\right.$，
∴△ABO≌△DBO（SAS），
∴DO=AO=5，
∴OF=$\sqrt{O{D}^{2}-D{F}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3，
DA=$\sqrt{D{F}^{2}+A{F}^{2}}$=$\sqrt{{4}^{2}+（5+3）^{2}}$=4$\sqrt{5}$，
∴AB=DB=2$\sqrt{5}$．
∵∠DBE=∠DFA=90°，∠BDE=∠FDA，
∴△BDE∽△FDA，
∴$\frac{DE}{DA}=\frac{DB}{DF}$，
∴DE=$\frac{DA•DB}{DF}$=10，
∴EF=DE-DF=10-4=6．
综上所述：EF的长度为$\frac{3}{2}$或6．
故答案为：$\frac{3}{2}$或6．

点评 本题考查了相似三角形的判定及性质、勾股定理以及等腰三角形的性质，解题的关键是利用相似三角形的性质求出DE的长度．本题属于中档题，难度不大，但用到的知识点较多，稍显繁杂，不过好在本题是填空题，可结合图形直接寻找DE的长度，降低了难度．