题目内容
5.在函数y=$\frac{1}{\sqrt{x+1}}$中,自变量x的取值范围是x>-1.分析 根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:由题意得,x+1>0,
解得x>-1.
故答案为:x>-1.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
15.若|3x+2y-4|+27(5x+6y)2=0,则x,y的值分别是( )
| A. | $\left\{\begin{array}{l}{x=6}\\{y=-5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-\frac{5}{2}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-\frac{11}{2}}\end{array}\right.$ |
 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数.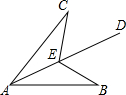 如图,AD平分∠BAC,点E在射线AD上,∠BED=∠CED,求证:AB=AC.
如图,AD平分∠BAC,点E在射线AD上,∠BED=∠CED,求证:AB=AC. 如图,直线MA∥NB,∠A=68°,∠B=40°,则∠P=28°.
如图,直线MA∥NB,∠A=68°,∠B=40°,则∠P=28°.