题目内容
1．下列命题：①无理数都是无限小数；②$\sqrt{16}$的平方根是±4；③等腰三角形的对称轴是它顶角的平分线；④三角形三边垂直平分线的交点一定在这个三角形的内部，正确的有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据无理数的定义，算术平方根的定义，平方根的定义，等腰三角形的对称性以及三角形的外心的位置对各小题分析判断即可得解．
解答 解：①无理数都是无限小数，正确；
②$\sqrt{16}$=4，所以，$\sqrt{16}$的平方根是±2，故本小题错误；
③等腰三角形的对称轴是它顶角的平分线所在的直线，故本小题错误；
④三角形三边垂直平分线的交点一定在这个三角形的内部，错误，等腰直角三角形三边垂直平分线的交点在斜边的中点，故本小题错误；
综上所述，命题正确的是①共1个．
故选A．
点评 本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
练习册系列答案
智慧小复习系列答案
相关题目
11．反比例函数y=$\frac{k}{x}$的图象生经过点（1，-2），则k的值为（ ）
| A． | -1 | B． | -2 | C． | 1 | D． | 2 |
12．下列二次根式中，最简二次根式是（ ）
| A． | $\sqrt{2{x}^{2}}$ | B． | $\sqrt{5}$ | C． | $\sqrt{8}$ | D． | $\sqrt{\frac{1}{x}}$ |
16．
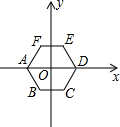如图，以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系，顶点A，D在x轴上，则点C的坐标为（ ）
如图，以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系，顶点A，D在x轴上，则点C的坐标为（ ）| A． | （1，-2） | B． | （1，-$\sqrt{2}$） | C． | （1，-$\sqrt{3}$） | D． | （-1，-$\sqrt{3}$） |
6．方程（x-1）（x+2）=x-1的解是（ ）
| A． | -2 | B． | 1，-2 | C． | -1，1 | D． | -1，3 |
13．下列说法错误的是（ ）
| A． | 四边形的内角和与外角和相等 | |
| B． | 五边形的每一个内角都是108° | |
| C． | 六边形的内角和等于其外角和的2倍 | |
| D． | 从n边形的一个顶点出发可以引（n-3）条对角线 |
10．如果不等式组$\left\{\begin{array}{l}{x+7＜3x-7}\\{x＞n}\end{array}\right.$的解集是x＞7，则n的取值范围是（ ）
| A． | n=7 | B． | n＜7 | C． | n≥7 | D． | n≤7 |
11．
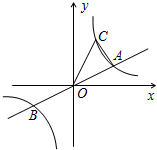如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）交于A、B两点，点B的坐标为（-4，-2），C为双曲线y=$\frac{k}{x}$（k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为（ ）
如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）交于A、B两点，点B的坐标为（-4，-2），C为双曲线y=$\frac{k}{x}$（k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为（ ）| A． | （2，4） | B． | （1，8） | C． | （2，4）或（1，8） | D． | （2，4）或（8，1） |