题目内容
11.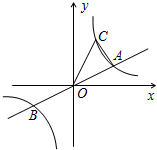 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=$\frac{k}{x}$(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=$\frac{k}{x}$(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )| A. | (2,4) | B. | (1,8) | C. | (2,4)或(1,8) | D. | (2,4)或(8,1) |
分析 首先利用待定系数法即可解决.过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,根据S△AOC=S△COF+S梯形ACFE-S△AOE=6,列出方程即可解决.
解答 解:∵点B(-4,-2)在双曲线y=$\frac{k}{x}$上,
∴$\frac{k}{-4}$=-2,
∴k=8,
∴双曲线的函数解析式为y=$\frac{8}{x}$.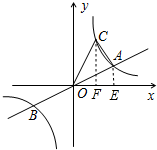
过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
∵正比例函数与反比例函数的交点A、B关于原点对称,
∴A(4,2),
∴OE=4,AE=2,
设点C的坐标为(a,$\frac{8}{a}$),则OF=a,CF=$\frac{8}{a}$,
当a<4时,则S△AOC=S△COF+S梯形ACFE-S△AOE,
=$\frac{1}{2}$×a×$\frac{8}{a}$+$\frac{1}{2}$(2+$\frac{8}{a}$)(4-a)-$\frac{1}{2}$×4×2
=$\frac{16-{a}^{2}}{a}$,
∵△AOC的面积为6,
∴$\frac{16-{a}^{2}}{a}$=6,
整理得a2+6a-16=0,
解得a=2或-8(舍弃),
∴点C的坐标为(2,4).
当a>4时,则S△AOC=S△COF+S梯形ACFE-S△AOE,
=$\frac{1}{2}$×a×$\frac{8}{a}$+$\frac{1}{2}$(2+$\frac{8}{a}$)(a-4)-$\frac{1}{2}$×4×2
=$\frac{{a}^{2}-16}{a}$,
∵△AOC的面积为6,
∴$\frac{{a}^{2}-16}{a}$=6,
整理得a2-6a-16=0,
解得a=-2(舍去)或8,
∴点C的坐标为(8,1).
故选D.
点评 本题考查反比例函数与一次函数交点、解题的关键是熟练掌握待定系数法,学会利用分割法求四边形面积,学会用方程的思想思考问题,属于中考常考题型.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{17}$ |
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
| A. | -2+a<-2+b | B. | -$\frac{a}{2}$<-$\frac{b}{2}$ | C. | -2a<-2b | D. | a-3>b-3 |
| A. | 100元 | B. | 120元 | C. | 140元 | D. | 160元 |
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -6 | D. | $\frac{3}{2}$ |