题目内容
5.已知将(x3+mx+n)(x2-3x+4)乘开的结果不含x2项,并且x3的系数为2.(1)求m、n的值;
(2)当m、n取第(1)小题的值时,求(m+n)(m2-mn+n2)的值.
分析 (1)先利用多项式乘法法则把多项式展开,那么原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.由于展开后不含x2项,并且x3的系数为2,由此可以得到4+m=2,-3m+n=0,解方程组即可以求出m、n.
②把m、n的值代入计算即可求解.
解答 解:(1)原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n
=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.
∵不含x2项,并且x3的系数为2,
∴4+m=2,-3m+n=0,
解得m=-2,n=-6;
(2)当m=-2,n=-6时,
(m+n)(m2-mn+n2)
=(-2-6)×(4-12+36)
=-8×28
=-224.
点评 考查了多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.同时考查了多项式的项的定义.

练习册系列答案
相关题目
10.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC的长为( )
| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$+3 | C. | 4$\sqrt{3}$-3 | D. | 4$\sqrt{3}$+3或4$\sqrt{3}$-3 |
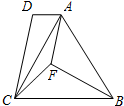 如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,CA是∠DCF的平分线.求证:AF∥DC.
如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,CA是∠DCF的平分线.求证:AF∥DC.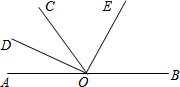 如图,点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,若∠COE等于64°,则∠AOD等于26度.
如图,点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,若∠COE等于64°,则∠AOD等于26度.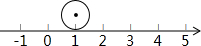 如图,把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴滚动一周,此时点A表示的数是1-π或1+π..
如图,把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴滚动一周,此时点A表示的数是1-π或1+π..