题目内容
10.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC的长为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$+3 | C. | 4$\sqrt{3}$-3 | D. | 4$\sqrt{3}$+3或4$\sqrt{3}$-3 |
分析 过A作BC的垂线,设垂足为D.首先在Rt△ABD中,求出AD的长,进而可在两个直角三角形中求出CD、BD的长;由于∠C可能是锐角也可能是钝角,因此要分类求解.
解答 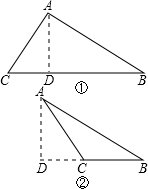 解:如图,过A作AD⊥BC(或BC的延长线)于D点.
解:如图,过A作AD⊥BC(或BC的延长线)于D点.
(1)如图①,Rt△ABD中,AB=8,∠ABC=30°,
∴AD=4,BD=4$\sqrt{3}$.
在Rt△ACD中,AC=5,AD=4,
由勾股定理,得:CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=3.
∴BC=CD+BD=4$\sqrt{3}$+3;
(2)如图②,同(1)可求得:
CD=3,BD=4$\sqrt{3}$.
则BC=BD-CD=4$\sqrt{3}$-3.
综上,BC=4$\sqrt{3}$±3.
故选:D.
点评 此题主要考查了勾股定理的应用、解直角三角形中三角形函数定义以及分类讨论的思想.在两个直角三角形有公共边时,先求出这条公共边是解答此类题的一般思路.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
2.已知事件A为必然事件,则概率P(A)的值( )
| A. | 等于0 | B. | 大于1 | C. | 等于1 | D. | 0<P(A)<1 |
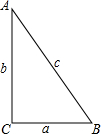 如图,在Rt△ABC中,两直角边长分别为a,b,斜边长为c,若Rt△ABC的面积为3,且a+b=5.则(1)ab=6;(2)c=$\sqrt{13}$.
如图,在Rt△ABC中,两直角边长分别为a,b,斜边长为c,若Rt△ABC的面积为3,且a+b=5.则(1)ab=6;(2)c=$\sqrt{13}$.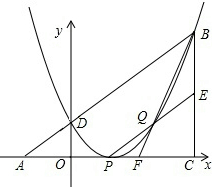 已知Rt△ABC在平面直角坐标系中如图所示,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.
已知Rt△ABC在平面直角坐标系中如图所示,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.