题目内容
14. 如图所示,AB是⊙O的直径,AB=8cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.
如图所示,AB是⊙O的直径,AB=8cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.
分析 根据角平分线的定义得到∠ADC=30°,由圆周角定理得到∠ABC=∠ADC=30°,由AB是⊙O的直径,AB=8cm,得到∠ACB=90°,于是得到结论.
解答 解:∵∠ADE=60°,DC平分∠ADE,
∴∠ADC=30°,
∴∠ABC=∠ADC=30°,
∵AB是⊙O的直径,AB=8cm,
∴∠ACB=90°,
∴AC=$\frac{1}{2}$AB=4cm,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4$\sqrt{3}$cm.
点评 本题考查了圆周角定理,特殊角的三角函数,解直角三角形,熟练掌握圆周角定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列变形中正确的是( )
| A. | $\frac{5a}{3b}$=$\frac{25{a}^{2}}{9{b}^{2}}$ | B. | -$\frac{c}{-a+b}$=$\frac{c}{a+b}$ | ||
| C. | $\frac{6a-5}{7-b}$=$\frac{5-6a}{b-7}$ | D. | $\frac{a-b}{a}$=$\frac{{a}^{2}-{b}^{2}}{a(a+b)}$ |
 在⊙O中,弦AC⊥BD,垂足为P.过点P的直线和AB垂直于H,交CD于M.求证:MC=MD.
在⊙O中,弦AC⊥BD,垂足为P.过点P的直线和AB垂直于H,交CD于M.求证:MC=MD.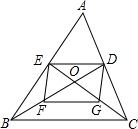 如图所示,在△ABC中,中线BD、CE相交于点0,点F、G分别为0B、OC的中点,求证:O是线段EG、DF的中点.
如图所示,在△ABC中,中线BD、CE相交于点0,点F、G分别为0B、OC的中点,求证:O是线段EG、DF的中点.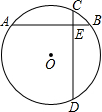 如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径.
如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径. 如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.