题目内容
9.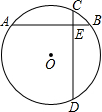 如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径.
如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径.
分析 作OG⊥CD于G,OF⊥AB于F,由相交弦定理得出DE•CE=AE•BE,求出DE=15,得出CD=CE+DE=16,由垂径定理得出得出AF=BF=$\frac{1}{2}$AB=4,DG=$\frac{1}{2}$CD=8,得出EF=BF-BE=1,证出四边形OGEF为矩形,得出OG=EF=1,在Rt△ODG中,由勾股定理求出OD即可.
解答 解:作OG⊥CD于G,OF⊥AB于F,如图所示: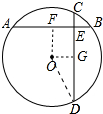
由相交弦定理得:DE•CE=AE•BE,即DE×1=5×3,
∴DE=15,
∴CD=CE+DE=16,∵OF⊥AB,AB=AE+BE=8,
∴AF=BF=$\frac{1}{2}$AB=4,
∴EF=BF-EE=4-3=1,
又OG⊥CD,OF⊥AB,CD⊥AB,
∴∠OGE=∠GEF=∠OFE=90°,DG=$\frac{1}{2}$CD=8,
∴四边形OGEF为矩形,
∴OG=EF=1,
在Rt△ODG中,OG=1,CG=8,
根据勾股定理得:OD=$\sqrt{O{G}^{2}+D{G}^{2}}$=$\sqrt{{1}^{2}+{8}^{2}}$=$\sqrt{65}$,
则圆O的半径为$\sqrt{65}$.
点评 此题考查了相交弦定理、垂径定理、勾股定理、矩形的判定与性质;根据图形作出相应的辅助线是解本题的关键.

练习册系列答案
相关题目
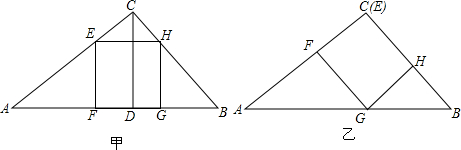
19.下列图形中不具有稳定性是( )
| A. |  | B. |  | C. |  | D. |  |

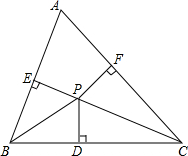 已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD,PE,PF分别垂直于BC,AC,AB于D,E,F三点.求证:PD=PE=PF.
已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD,PE,PF分别垂直于BC,AC,AB于D,E,F三点.求证:PD=PE=PF. 如图所示,AB是⊙O的直径,AB=8cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.
如图所示,AB是⊙O的直径,AB=8cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长. 如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.
如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.