题目内容
19. 如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
分析 延长AD至E,使ED=AD=2,则AE=4,由SAS证明△ABD≌△ECD,得出BE=AC=3,利用勾股定理逆定理证得△ABE是直角三角形,得出△ABC的面积=△ABE的面积,即可得出结果.
解答 解:延长AD至E,使ED=AD=2,连接BE,如图所示:
则AE=4,
∵D是BC的中点,
∴BD=CD,
在△BED和△ACD中,
$\left\{\begin{array}{l}{BD=CD}&{\;}\\{∠BDE=∠CDA}&{\;}\\{ED=AD}&{\;}\end{array}\right.$,
∴△BED≌△ACD(SAS),
∴BE=AC=3,
∵AE=4,AB=5,BE=3,
∴AE2+BE2=AB2,
∴△ABE是直角三角形,
∴△ABC的面积=△ABE的面积=$\frac{1}{2}$×3×4=6.
点评 此题考查三角形全等的判定与性质、勾股定理逆定理的运用、三角形的面积计算方法;通过作辅助线证明三角形全等,进一步证出直角三角形是解决问题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图,圆锥的轴截面(图中的△SAB)是等边三角形,高为4$\sqrt{3}$,求这个圆锥的侧面积和全面积(结果保留π)
如图,圆锥的轴截面(图中的△SAB)是等边三角形,高为4$\sqrt{3}$,求这个圆锥的侧面积和全面积(结果保留π) 已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AD=CB.
已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AD=CB. 如图所示,AB是⊙O的直径,AB=8cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.
如图所示,AB是⊙O的直径,AB=8cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.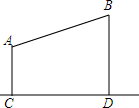 因需要,计划在山顶A,B处架绳索设一绳索滑道.已测到山顶A的海拔高度AC为300米,山顶B的海拔高度BD为800米,山顶A,B之间的水平宽度CD为1200米,问这一绳索至少需要多少米?
因需要,计划在山顶A,B处架绳索设一绳索滑道.已测到山顶A的海拔高度AC为300米,山顶B的海拔高度BD为800米,山顶A,B之间的水平宽度CD为1200米,问这一绳索至少需要多少米?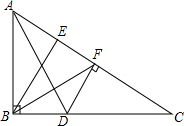 如图,在Rt△ABC中,∠ABC=90°,BE⊥AC,垂足为点E,AD平分∠BAC,DF∥BE,EF=4,求点F到BC的距离.
如图,在Rt△ABC中,∠ABC=90°,BE⊥AC,垂足为点E,AD平分∠BAC,DF∥BE,EF=4,求点F到BC的距离.