题目内容
16.现有三张分别标有数字1、2、6的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a(不放回),再从中任意抽取一张,将上面的数字记为b,这样的数字a,b能使关于x的一元二次方程x2-2(a-3)x-b2+9=0有两个正根的概率为$\frac{1}{6}$.分析 首先用列表法或树状图得到所有可能的结果,在根据满足条件的事件数,在整理时要借助于根与系数之间的关系,根的判别式,要进行讨论得到结果.
解答 解:画树形图得: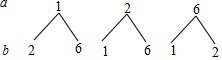
∵方程有两个正根,
∴由韦达定理得 2(a-3)>0,-b2+9>0,
解得a>3,b<3,
若b=2,9-b2=5 要使方程有两个正根,判别式=4(a-3)2-4×5>0 (a-3)2>5,解得,a=6;
若b=1,9-b2=8 判别式=4(a-3)2-4×8>0 (a-3)2>8,解得,a=6,
∴a,b只有两种情况满足要求:a=6,b=1,
∴能使关于x的一元二次方程x2-2(a-3)x-b2+9=0有两个正根的概率=$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
5.a是一位数,b是两位数,如果把a置于b的左边,那么所得的三位数可表示为( )
| A. | 100a+b | B. | ab | C. | 100ab | D. | 100a+10b |


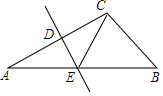 如图,△ABC中,AB=10,BC=6,边AC的垂直平分线分别交AB、AC于点E、D,则△BCE的周长为16.
如图,△ABC中,AB=10,BC=6,边AC的垂直平分线分别交AB、AC于点E、D,则△BCE的周长为16.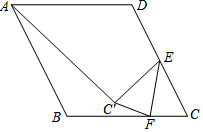 如图,菱形ABCD中,AB=4,∠B=120°,点E为CD的中点,F为BC边上一动点,将△EFC延EF折叠得到△EFC′,连接AC′,则AC′的最小值为2$\sqrt{7}$-2.
如图,菱形ABCD中,AB=4,∠B=120°,点E为CD的中点,F为BC边上一动点,将△EFC延EF折叠得到△EFC′,连接AC′,则AC′的最小值为2$\sqrt{7}$-2. 如图所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-$\frac{1}{2}$时,y取最大值$\frac{25}{4}$.
如图所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-$\frac{1}{2}$时,y取最大值$\frac{25}{4}$.