题目内容
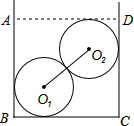某人用如下方法测一钢管的内径：将一小段钢管竖直放在平台上，向内放入两个半径为5cm的钢球，测得上面一个钢球顶部高DC=16cm（钢管的轴截面如图所示），求钢管的内直径AD的长．
考点：相切两圆的性质
专题：
分析：根据切线的性质和两圆外切的性质，可以构造一个直角三角形，解直角三角形即可．
解答：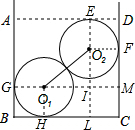
解：如图，作O2F⊥DC于F，O2E⊥AD于E，O1G⊥AB于G，O1H⊥BC于H，O1M⊥DC于M．
根据题意得出：正方形BHO1G和正方形EO2FD，
∴BG=DE=球的半径，然后可得出GM∥BC，EL∥DC，
∴∠O2IO1=90°，
直角三角形的斜边是O2O1=10，
其中一条直角边O2I=EL-EO2-IL=DC-EO2-O1H=16-10=6，
则根据勾股定理得另一条直角边O1I=8．
则钢管的直径AD=GM=GO1+O1I+IM=8+5+5=18（cm）．
解：如图，作O2F⊥DC于F，O2E⊥AD于E，O1G⊥AB于G，O1H⊥BC于H，O1M⊥DC于M．根据题意得出：正方形BHO1G和正方形EO2FD，
∴BG=DE=球的半径，然后可得出GM∥BC，EL∥DC，
∴∠O2IO1=90°，
直角三角形的斜边是O2O1=10，
其中一条直角边O2I=EL-EO2-IL=DC-EO2-O1H=16-10=6，
则根据勾股定理得另一条直角边O1I=8．
则钢管的直径AD=GM=GO1+O1I+IM=8+5+5=18（cm）．
点评：此题主要考查了相切两圆的性质以及勾股定理等知识，此类题主要是构造一个直角三角形，根据勾股定理进行计算是解题关键．
练习册系列答案
相关题目
如图，在⊙O中，直径AB⊥弦CD于点E．若BE=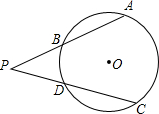
如图，P为⊙O外一点，∠APC的两边分别交⊙O于点A，B和C，D．如果PA=PC，求证：AB=CD．
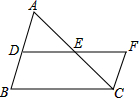在△ABC中，点D，E分别是AB，AC的中点，连接DE并延长到点F，使EF=DE，连接CF．
如图，已知BC与DE交于点M，求∠A+∠B+∠C+∠D+∠E+∠F的度数．
如图，在平面直角坐标系中有△ABC．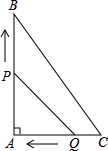
如图，在Rt△ABC中，∠A=90°，AB=8cm，AC=6cm．点P从点A出发，沿AB方向以2cm/s的速度向点B运动；同时点Q从点C出发，沿CA方向以1cm/s的速度向点A运动．其中一个动点到达终点时，另一个动点也停止运动．