��Ŀ����
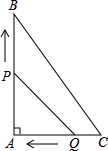 ��ͼ����Rt��ABC�У���A=90�㣬AB=8cm��AC=6cm����P�ӵ�A��������AB������2cm/s���ٶ����B�˶���ͬʱ��Q�ӵ�C��������CA������1cm/s���ٶ����A�˶�������һ�����㵽���յ�ʱ����һ������Ҳֹͣ�˶���
��ͼ����Rt��ABC�У���A=90�㣬AB=8cm��AC=6cm����P�ӵ�A��������AB������2cm/s���ٶ����B�˶���ͬʱ��Q�ӵ�C��������CA������1cm/s���ٶ����A�˶�������һ�����㵽���յ�ʱ����һ������Ҳֹͣ�˶�����1�����APQ�����S��cm2�����ڶ�����˶�ʱ��t��s���ĺ�������ʽ����д��t��ȡֵ��Χ��
��2����tΪ��ֵʱ����APQ���������������Ƕ��٣�
���㣺���κ�����Ӧ��
ר�⣺
��������1������t��ʾ��AP��AQ�����������ε�������㷽���г�����t�ĺ�����ϵʽ��
��2�����ã�1���еĺ���̽�����ֵ���⼴�ɣ�
��2�����ã�1���еĺ���̽�����ֵ���⼴�ɣ�
����⣺��1��AP=2t��AQ=6-t��
S=
AP•AQ=
��2t��6-t��=-t2+6t��0��t��4����
��2����S=-t2+6t=-��t-3��2+9��
��t=3ʱ����APQ����������������9��
S=
| 1 |
| 2 |
| 1 |
| 2 |
��2����S=-t2+6t=-��t-3��2+9��
��t=3ʱ����APQ����������������9��
������������Ҫ������κ�����Ӧ�ã����������ε�����������������ú���̽����ֵ���⣮

��ϰ��ϵ�д�
�����Ŀ
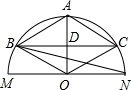 ��ͼ��MNΪ��ԲO��ֱ�����뾶0A��MN��DΪOA���е㣬����D��BC��MN����֤��
��ͼ��MNΪ��ԲO��ֱ�����뾶0A��MN��DΪOA���е㣬����D��BC��MN����֤�� ��ͼ����ֱ��MN����һ��P��ʹ��P��ֱ��AB��ֱ��CD�ľ�����ȣ�
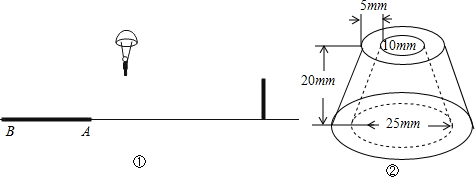
��ͼ����ֱ��MN����һ��P��ʹ��P��ֱ��AB��ֱ��CD�ľ�����ȣ�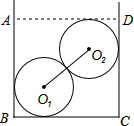 ij�������·�����һ�ֹܵ��ھ�����һС�θֹ���ֱ����ƽ̨�ϣ����ڷ�������
ij�������·�����һ�ֹܵ��ھ�����һС�θֹ���ֱ����ƽ̨�ϣ����ڷ�������