题目内容
6.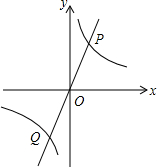 如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.
如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.(1)求反比例函数的解析式;
(2)如果0A=2,试求点Q的坐标.
分析 (1)由反比例函数y=$\frac{k}{x}$的比例系数k的几何意义,根据△AOC的面积得出$\frac{1}{2}$|k|=3,从而求出k的值,即得到这个反比例函数的解析式.
(2)先求得P的坐标,然后根据反比例函数与正比例函数的图象特征,可知P、Q两点关于原点对称,即可求得Q的坐标.
解答 解:(1)∵△POC的面积=$\frac{1}{2}$|k|=3,
∴k=6.
故这个反比例函数的解析式为y=$\frac{6}{x}$.
(2)∵OA=2,
∴P的横坐标为2,
代入y=$\frac{6}{x}$得y=3,
∴P(2,3),
∵正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,
∴P、Q两点关于原点对称,
∴Q(-2,-3).
点评 本题主要考查了反比例函数的比例系数k的几何意义:反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=$\frac{1}{2}$|k|.

练习册系列答案
相关题目
16.若方程$\frac{x+1}{2}-\frac{2x-1}{5}$=0与方程x+$\frac{6a-x}{2}=\frac{a}{3}$的解相同,则a=( )
| A. | $\frac{21}{16}$ | B. | $\frac{63}{16}$ | C. | -$\frac{21}{16}$ | D. | -$\frac{63}{16}$ |
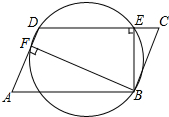 如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.
如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.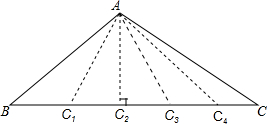 如图所示,△ABC的底边BC上的高是6cm,当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.在这个变化过程中,变量是BC,常量是6cm.
如图所示,△ABC的底边BC上的高是6cm,当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.在这个变化过程中,变量是BC,常量是6cm.