题目内容
12. 已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )
已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |
分析 过点D作DE⊥BC于E,延长AB到A′,使得A′B=AB,连接A′D交BC于P,此时PA+PD最小,利用已知条件可证明此时BP为△AA′D的中位线,进而可求出BP的长.
解答 解:过点D作DE⊥BC于E,
∵AD∥BC,AB⊥BC,
∴四边形ABED是矩形,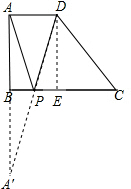
∴BE=AD=4,
∵BC=CD=5,
∴EC=3,
∴AB=DE=4,
延长AB到A′,使得A′B=AB,连接A′D交BC于P,此时PA+PD最小,即当P在AD的中垂线上,PA+PD取最小值,
∵B为AA′的中点,BP∥AD
∴此时BP为△AA′D的中位线,
∴BP=$\frac{1}{2}$AD=2,
故选B.
点评 本题考查了轴对称-线段最短的问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点,证明BP为△AA′D的中位线是解题本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
2.下列各组数中不能作为直角三角形的三边长的是( )
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 0.7,2.4,2.5 | C. | 6,8,10 | D. | 9,12,15 |
14.若点P(a,b)在第二象限,则点P(b,a)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=$\frac{72}{5}$.其中所有正确结论的个数是( )
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=$\frac{72}{5}$.其中所有正确结论的个数是( )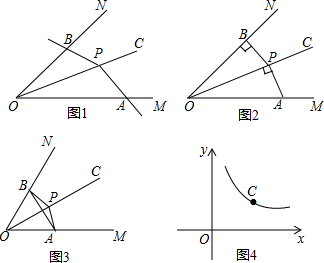
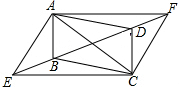 如图,已知四边形AECF是平行四边形,点B,D在对角线EF上,且BE=DF,用向量的加法证明:四边形ABCD是平行四边形.
如图,已知四边形AECF是平行四边形,点B,D在对角线EF上,且BE=DF,用向量的加法证明:四边形ABCD是平行四边形.