题目内容
3.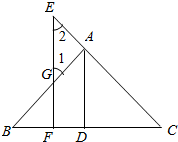 如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠ADC=90°,∠EFC=90°(垂的定义)
∴∠ADC=∠EFC
AD∥EF
∴∠1=∠DAB
∠2=∠DAC
∵∠1=∠2(已知)
∴∠DAB=∠DAC
∴AD平分∠BAC(角平分线定义)
分析 由∠1=∠2得出△AEG是等腰三角形,根据等腰三角形的性质得出∠E=∠AGE,根据AD⊥BC,EF⊥BC推出AD∥EF,根据平行线的性质得出∠AGE=∠DAB,∠E=∠DAC,推出∠DAB=∠DAC即可.
解答 证明:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直的定义),
∴∠ADC=∠EFC,
AD∥EF,
∴∠1=∠DAB,∠2=∠DAC,
∵∠1=∠2,
∴∠DAB=∠DAC,
即AD平分∠BAC(角平分线定义)
故答案为:∠ADC;∠EFC;AD;EF;∠DAB;∠DAC;∠DAB;∠DAC.
点评 本题考查了等腰三角形的性质,垂直定义,平行线的性质和判定,主要考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.设(2a+3b)2=(2a-3b)2+A,则A=( )
| A. | 6ab | B. | 12ab | C. | 0 | D. | 24ab |
11.下列各式由左边到右边的变形中,是分解因式的为( )
| A. | -xy2+2xy-3y=-y(xy-2x+3) | B. | 2x2-xy-x=2x(x-y-1) | ||
| C. | (y-2)2=y2-4y+4 | D. | x2-x-3=x(x-1)-3 |
18.16的平方根是( )
| A. | 4 | B. | 8 | C. | ±4 | D. | 不存在 |