题目内容
13.观察分式$\frac{1}{a},-\frac{2}{{a}^{2}},\frac{4}{{a}^{3}}$,-$\frac{8}{{a}^{4}}$,$\frac{16}{{a}^{5}}$,…根据其中规律,这一组分式的第10个分式是-$\frac{512}{{a}^{10}}$,第n个分式是(-1)n+1$\frac{{2}^{n-1}}{{a}^{n}}$.分析 分析题干中的式子:分母为:a1,a2,a3,a4…则第n项的分母应为an,分子:21-1,22-1,23-1…则第n项的分子应为:2n-1.由给定的分式可以看出:奇数项为正,偶数项为负.
解答 解:由分析可得第10个分式的分母为:a10,分子为:210-1,符号为负.则第10个分式为:-$\frac{{2}^{9}}{{a}^{10}}$=-$\frac{512}{{a}^{10}}$.
第n个分式是:(-1)n+1$\frac{{2}^{n-1}}{{a}^{n}}$.
故答案是:-$\frac{512}{{a}^{10}}$;(-1)n+1$\frac{{2}^{n-1}}{{a}^{n}}$.
点评 本题考查了分式的定义.对于找规律的题应该观察有哪些部分在变化,总结各部分的变化规律从而得到整个式子的变化规律.

练习册系列答案
相关题目
3.下列选项中互为相反数的是( )
| A. | 0.2和2.0 | B. | -0.2和2.0 | C. | 0.2和-$\frac{1}{5}$ | D. | 0.2和5 |
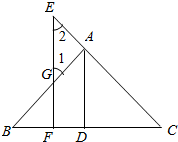 如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.