题目内容

13．若凸（4n+2）边形A1A2A3…A4n+2（n为自然数）的每个内角都是30°的整数倍，且∠A1=∠A2=∠A3=90°，求n的值．

分析 由任意多边形的外角和为360°，可求得其它个角的外角和为90°，由多边形的每个外角和也是30的倍数可知另外最多还有3个外角和，故此4n+2≤6．

解答 解：∵∠A1=∠A2=∠A3=90°，
∴这3个角对应的外角和的和是270°．
∵任意多边形的外角和为360°，
∴这个多边形其它几个外角和为90°．
∵该多边形每个内角都是30的倍数，
∴它们的每个外角和也是30的倍数．
∵90°÷30°=3．
∴4n+2≤6．
解得n≤1．
又∵4n+2为正整数，
∴n=1．

点评 本题主要考查的是多边形的内角、外角，利用多边形的外角和是360°求得多边形的边数的范围是解题的关键．

练习册系列答案
相关题目
3．化简：$\frac{x}{{x}^{3}+{x}^{2}y+x{y}^{2}+{y}^{3}}$+$\frac{y}{{x}^{3}-{x}^{2}y+x{y}^{2}-{y}^{3}}$+$\frac{1}{{x}^{2}-{y}^{2}}$-$\frac{1}{{x}^{2}+{y}^{2}}$-$\frac{{x}^{3}+3{y}^{2}}{{x}^{4}-{y}^{4}}$．
4．已知A=3a2+b2-5ab；B=2ab-3b2+4a2，当a=-$\frac{1}{2}$，b=2时，求-2A-3B的值．
1．用乘方形式表示结果：
（1）（-2）2014+（-2）2015=-22014；
（2）（-$\frac{2}{3}$）2015×$（-\frac{9}{2}）$2015=32015．
8．（1）如图①所示，在△ABC中，∠ABC的平分线BO与∠ACB的平分线CO交于点O，试探求∠A与∠BOC的数量关系．
（2）如图②，在△ABC中，D是边AB延长线上一点，E是边AC延长线上一点，∠CBD的平分线BO与∠BCE的平分线CO交于点O，试探求：
①∠A与∠BOC的数量关系；
②按角的大小来判断△BOC的形状．
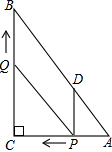18．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ．点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．
（1）直接用含t的代数式分别表示：QB=8-2t，PD=$\frac{4}{3}$t．
（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由．并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度．
5．在Rt△ABC中，∠C=90°，∠A的对边为a，已知∠A和边a，求边c，则下列关系式中，正确的是（　　）
A．c=asinAB．c=$\frac{a}{sinA}$C．a=btanAD．c=$\frac{a}{cosA}$
2．如图，长方形ABCD中放置9个形状、大小都相同的小长方形，相关数据图中所示，则图中阴影部分的面积为多少．
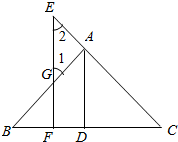3．如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．
求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠ADC=90°，∠EFC=90°（垂的定义）
∴∠ADC=∠EFC
AD∥EF
∴∠1=∠DAB
∠2=∠DAC
∵∠1=∠2（已知）
∴∠DAB=∠DAC
∴AD平分∠BAC（角平分线定义）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网