题目内容
12.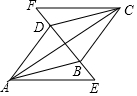 如图,将四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF,若AE∥CF且AE=CF.
如图,将四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF,若AE∥CF且AE=CF.(1)求证:△ABE≌△CDF;
(2)若AC⊥EF,求证:四边形ABCD是菱形.
分析 (1)根据SAS可证△ABE≌△CDF;
(2)根据全等三角形的性质和平行四边形的判定可得四边形ABCD是平行四边形,再根据菱形的判定即可求解.
解答 证明:(1)∵AE∥CF,
∴∠E=∠F,
在△ABE与△CDF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠E=∠F}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF;
(2)∵△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,
∴∠ABD=∠CDB,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∵AC⊥EF,即AC⊥DB,
∴平行四边形ABCD是菱形.
点评 此题主要考查了平行四边形的性质和判定、菱形的判定以及全等三角形的判定与性质,关键是掌握平行四边形的判定、菱形的判定方法和全等三角形的判定方法.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 已知∠MAN和线段a,用尺规作等腰△ABC,使顶角为∠MAN,底边上的中线长为a,并写出所依据的主要定理.
已知∠MAN和线段a,用尺规作等腰△ABC,使顶角为∠MAN,底边上的中线长为a,并写出所依据的主要定理.
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题: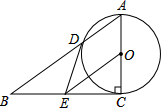 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E为BC的中点,连接DE.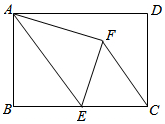 如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.
如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.