题目内容
3．解不等式（或组），并把解集在数轴上表示出来（1）$\frac{x-1}{3}$-$\frac{3x+5}{6}$≥-2
（2）$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3（x-1）＜8-x}\end{array}\right.$．
分析 （1）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．
（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：（1）去分母，得：2（x-1）-（3x+5）≥-12，
去括号，得：2x-2-3x-5≥-12，
移项、合并同类项，得：-x≥-5，
系数化为1，得：x≤5，
表示在数轴上如下：
（2）解不等式$\frac{x-3}{2}$+3≥x+1，得：x≤1，
解不等式1-3（x-1）＜8-x，得：x＞-2，
∴不等式组的解集为-2＜x≤1，
表示在数轴上如下：
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．某中学七、八年级各选派10名选手参加学校举办的知识竞赛，竞赛计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀．七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示．
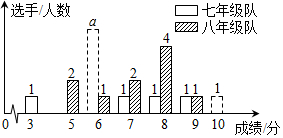
（1）请依据图表中的数据，求出a的值；并直接写出表格中m，p，q的值；
（2）有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由、
| 队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
| 八年级 | 7.1 | p | q | 1.69 | 80% | 10% |
（1）请依据图表中的数据，求出a的值；并直接写出表格中m，p，q的值；
（2）有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由、
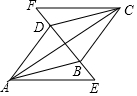如图，将四边形ABCD的对角线BD向两个方向延长，分别至点E和点F，且使BE=DF，若AE∥CF且AE=CF．