题目内容
20. 如图,在菱形ABCD中,BD=AB,求这个菱形的各个内角的度数.
如图,在菱形ABCD中,BD=AB,求这个菱形的各个内角的度数.
分析 由菱形的性质和已知条件易证△ABD是等边三角形,所以∠A的度数可求出,进而可求出菱形其他内角的度数.
解答 解:
∵四边形ABCD是菱形,
∴AB=AD,∠A=∠C,∠A+∠ADC=180°,
∵BD=AB,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴∠A=60°,
∴∠C=60°,
∴∠ABC=∠ADC=120°.
点评 本题考查了菱形的性质以及等边三角形的判定和性质,熟记菱形和等边三角形的各种性质是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
10.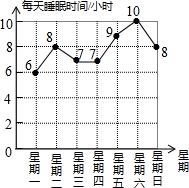 如今中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题,教育部规定,初中生每天的睡眠时间应为9个小时,鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有( )
如今中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题,教育部规定,初中生每天的睡眠时间应为9个小时,鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有( )
 如今中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题,教育部规定,初中生每天的睡眠时间应为9个小时,鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有( )
如今中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题,教育部规定,初中生每天的睡眠时间应为9个小时,鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有( )| A. | 1天 | B. | 2天 | C. | 3天 | D. | 4天 |
8.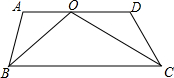 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )
 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
9.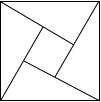 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )| A. | 13 | B. | 19 | C. | 25 | D. | 169 |
10.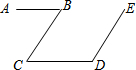 如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
 如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )| A. | 40° | B. | 60° | C. | 140° | D. | 160° |
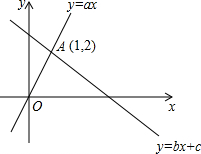 如图,函数y=ax和y=bx+c的图象相交于点A(1,2),则不等式ax>bx+c的解集为x>1.
如图,函数y=ax和y=bx+c的图象相交于点A(1,2),则不等式ax>bx+c的解集为x>1. 某公司销售智能机器人,每台售价为10万元,进价y(万元)与销量x(台)之间的函数关系的图象如图所示.
某公司销售智能机器人,每台售价为10万元,进价y(万元)与销量x(台)之间的函数关系的图象如图所示.