题目内容
8.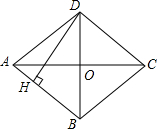 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.
分析 根据菱形的对角线互相垂直平分求出OA、OB,再根据勾股定理列式求出AB,然后利用菱形的面积列式计算即可得解.
解答 解:∵四边形ABCD是菱形,AC=8cm,BD=6cm,
∴AC⊥BD,OA=$\frac{1}{2}$AC=4cm,OB=$\frac{1}{2}$BD=3cm,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5cm.
∵DH⊥AB于H,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=AB•DH,
即$\frac{1}{2}$×8×6=5•DH,
解得DH=$\frac{24}{5}$.
故答案为$\frac{24}{5}$cm.
点评 本题考查了菱形的对角线互相垂直平分的性质,勾股定理,根据菱形的面积的两种表示方法列出方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.一个正方形的面积为21,它的边长为a,则a-1的边长大小为( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
13.下表是一文具店1~7月份数学作业本销售情况统计表:
观察表中数据可知,众数是200,中位数是300.
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 作业本/本 | 300 | 200 | 400 | 500 | 300 | 200 | 200 |
20.宇宙中光的传播速度最快,已知光的速度是每秒3×105km,则在5×10-3秒内,光线通过的距离是( )
| A. | 1500km | B. | 60km | C. | 150km | D. | 600km |
17.在同一平面内,直线AB与CD相交于点O,如果AB∥EF,那么CD与EF的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 无法确定 |
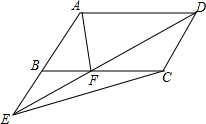 如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.
如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.