题目内容
15.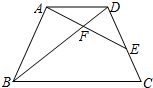 如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.
如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.(1)求证:△ADE∽△BAD;
(2)当BF=9时,求BC的长.
分析 (1)由已知条件可得梯形ABCD为等腰梯形,所以∠BAD=∠ADC,又因为∠EAD=∠ABD,所以可证明△ADE∽△BAD;
(2)延长AE交BC的延长线为G,由△ADF∽△BDA,利用相似的性质可求出DF=3,由△ADE∽△BAD,利用相似三角形的性质可求出DE=4.5,再根据平行线分线段成比例定理即可求出BC的长.
解答 (1)证明:∵AB=CD,AD∥BC,
∴梯形ABCD为等腰梯形,
∴∠BAD=∠ADC,
∵∠EAD=∠ABD,∠ADC=∠BAD,
∴△ADE∽△BAD;
(2)解:延长AE交BC的延长线为G,
∵△ADF∽△BDA,
∴DF:AD=AD:BD,
∴DF:6=6:(DF+9),
∴DF=3,
∵△ADE∽△BAD,
∴DE:AD=AD:AB,
∴DE:6=6:8,
∴DE=4.5,
∵CD=8
∴DE:CE=4.5:(8-4.5)=9:7,
∵AD∥BG,
∴AD:CG=DE:CE,
∴6:CG=9:7,
∴CG=$\frac{14}{3}$,
∵AD∥BG
∴AD:BG=DF:BF,
∴6:(BC+$\frac{14}{3}$)=3:9,
∴BC=$\frac{40}{3}$.
点评 本题考查了相似形的综合题,用到的知识点有等腰梯形的判定和性质、相似三角形的判定和性质、平行线分线段成比例定理,题目的综合性较强,难度中等,解题的关键是正确作出图形的辅助线,构造相似三角形,利用相似三角形的性质解答.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
10.下列关于x的方程中,无理方程是( )
| A. | ${x^2}+\sqrt{5}x+1=0$ | B. | $\sqrt{2}x+1=0$ | C. | $\sqrt{x+1}+\sqrt{2}=0$ | D. | $\sqrt{a-1}$+2x=7 |
20.宇宙中光的传播速度最快,已知光的速度是每秒3×105km,则在5×10-3秒内,光线通过的距离是( )
| A. | 1500km | B. | 60km | C. | 150km | D. | 600km |
4.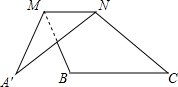 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )| A. | 88° | B. | 116° | C. | 126° | D. | 112° |
 如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.
如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.