题目内容
3．
将一个三角形和一个矩形按照如图的方式扩大，使他们的对应边之间的距离均为1，得到新的三角形和矩形，下列说法正确的是（ ）| A． | 新三角形与原三角形相似 | |
| B． | 新矩形与原矩形相似 | |
| C． | 新三角形与原三角形、新矩形与原矩形都相似 | |
| D． | 新三角形与原三角形、新矩形与原矩形都不相似 |
分析 根据相似三角形的判定定理、相似多边形的判定定理证明即可．
解答 
解：根据题意得：AB∥A′B′，AC∥A′C′，BC∥B′C′，
∴∠A=∠A′，∠B=∠B′，
∴△ABC∽△A′B′C′；
∵根据题意得：AB=CD=3，AD=BC=5，则A′B′=C′D′=3+2=5，A′D′=B′C′=5+2=7，
∴
$\frac{AD}{A′D′}$=$\frac{3}{7}$，$\frac{AB}{A′B′}$=$\frac{3}{5}$，
∴新矩形与原矩形对应边的比不相等，
∴新矩形与原矩形不相似，
故选：A．
点评 本题考查的是相似图形的判断，掌握对应角相等，对应边成比例的多边形，叫做相似多边形是解题的关键．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
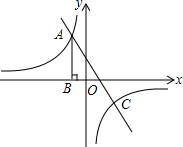如图，反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A，AB⊥x轴于点B，OB=1，AB=4．
如图，直线y=kx（k＞0）与双轴线y=$\frac{3}{x}$相交于A，B两点，作AC⊥x轴，垂足为C，连接BC，则△ABC的面积是3．