题目内容
2.在平面直角坐标系中,已知点P(1,1),在x轴的正半轴上找一点A,使得△AOP为等腰三角形,则点A的坐标为(1,0),(2,0)(写出满足条件的两个点A的坐标即可)分析 根据勾股定理求出OP的长,分OP为底和OA′为底两种情况,根据等腰三角形的判定定理和性质定理计算即可.
解答 解:∵点P的坐标为(1,1),
∴OP=$\sqrt{2}$, 作PA⊥x轴于A,则OA=AP,
作PA⊥x轴于A,则OA=AP,
∴△AOP为等腰三角形,
点A的坐标为(1,0),
以P为圆心,$\sqrt{2}$为半径作弧交x轴于A′,
则△AOP为等腰三角形,
点A的坐标为(2,0),
故答案为:(1,0),(2,0).
点评 本题考查了等腰三角形的判定,坐标与图形性质,熟练掌握等腰三角形的判定方法是解题的关键,解答时,注意分情况讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如果(x2-mx-n)(x-3)的乘积中不含x2项和x项,那么( )
| A. | m=0,n=0 | B. | m=-3,n=-9 | C. | m=-3,n=9 | D. | m=3,n=-9 |
10.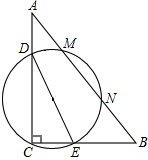 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{14}{5}$ |
17.若关于x的不等式3x<a+5与2x<4的解集相同,则a的值是( )
| A. | 1 | B. | 7 | C. | 2 | D. | 5 |
7. 如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
 如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )| A. | AE=CD | B. | AE>CD | C. | AE<CD | D. | 无法确定 |
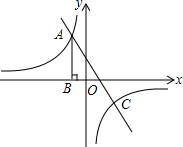 如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4.
如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4. 如图,直线y=kx(k>0)与双轴线y=$\frac{3}{x}$相交于A,B两点,作AC⊥x轴,垂足为C,连接BC,则△ABC的面积是3.
如图,直线y=kx(k>0)与双轴线y=$\frac{3}{x}$相交于A,B两点,作AC⊥x轴,垂足为C,连接BC,则△ABC的面积是3.