题目内容
6.若不等式$\left\{\begin{array}{l}{2x-a<1}\\{x-2b>3}\end{array}\right.$的解集为-1<x<1,求代数式(b-1)a+1的值.分析 首先解每个不等式,然后根据不等式组的解集,即可得到关于a和b的方程,求得a和b的值,进而求解.
解答 解:$\left\{\begin{array}{l}{2x-a<1…①}\\{x-2b>3…②}\end{array}\right.$,
解①得:x<$\frac{a+1}{2}$,
解②得:x>2b+3,
根据题意得:$\frac{a+1}{2}$=1,且2b+3=-1,
解得:a=1,b=-2,
则原式=(-3)2=9.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
11.某班50名同学积极参加赈灾捐款活动,下表是小明对全班捐款情况的统计表:
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?
| 捐款(元) | 10 | 15 | 30 |  | 50 | 60 |
| 人数 | 3 | 6 | 11 |  | 13 | 6 |
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?
 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}$x+6的图象分别交x、y轴于点A,B,与一次函数Y=kx的图象交于第一象限内的点C.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}$x+6的图象分别交x、y轴于点A,B,与一次函数Y=kx的图象交于第一象限内的点C.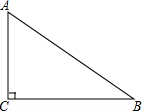 如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是8cm,点A到BC的距离是6cm,C到AB的距离是4.8cm.
如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是8cm,点A到BC的距离是6cm,C到AB的距离是4.8cm.