题目内容
14.如果x<-2,则$\sqrt{(x+2)^{2}}$=-x-2;化简$\frac{2x+2y}{5{a}^{2}b}$•$\frac{10a{b}^{2}}{{x}^{2}-{y}^{2}}$的结果为$\frac{4b}{a(x-y)}$..分析 (1)先求得x+2<0,然后利用$\sqrt{{a}^{2}}=|a|$绝对值进行化简即可;
(2)先将分式的分子分母进行分解,然后再约分、计算即可.
解答 解:(1)∵x<-2,
∴x+2<0.
∴$\sqrt{(x+2)^{2}}$=|x+2|=-x-2;
(2)原式=$\frac{2(x+y)}{5{a}^{2}b}•\frac{10a{b}^{2}}{(x+y)(x-y)}$=$\frac{4b}{a(x-y)}$.
故答案为:-x-2;$\frac{4b}{a(x-y)}$.
点评 本题主要考查的是二次根式的性质和分式的化简,掌握二次根式的性质和分式化简的方法和步骤是解题的关键.

练习册系列答案
相关题目
19.为了了解一批产品的质量,从中抽取300个产品进行检验,在这个问题中,被抽取的300个产品叫做( )
| A. | 总体 | B. | 个体 | C. | 总体的一个样本 | D. | 普查方式 |
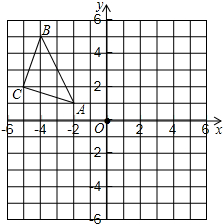 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).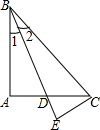 如图所示,已知在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于E,BD和CE有何数量关系?试说明.
如图所示,已知在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于E,BD和CE有何数量关系?试说明.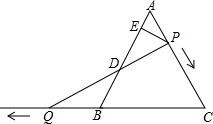 如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.
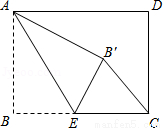
如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D. 如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD,若AE=AB,∠AEB=2∠ADB,求证:四边形ABCD是菱形.
如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD,若AE=AB,∠AEB=2∠ADB,求证:四边形ABCD是菱形.