题目内容
11.计算:(1)3$\sqrt{5}$-$\frac{1}{2}$$\sqrt{5}$+$\frac{3}{4}$$\sqrt{5}$
(2)(2$\sqrt{3}$+3$\sqrt{2}$)2(2$\sqrt{3}$-3$\sqrt{2}$)2
(3)$\frac{5}{6}$$\sqrt{10}$×6$\sqrt{7}$÷$\frac{2}{3}$$\sqrt{10}$÷$\frac{5}{\sqrt{7}}$
(4)($\frac{1}{\sqrt{2}-1}$)-1+($\sqrt{2}$)2×$\sqrt{6}$÷$\sqrt{3}$
(5)2$\sqrt{5}$-3$\sqrt{5}$+2${\;}^{\frac{3}{2}}$×$\sqrt{2}$+(1$\frac{7}{9}$)${\;}^{-\frac{1}{2}}$-(2$\frac{1}{4}$)${\;}^{\frac{1}{2}}$.
分析 (1)直接合并同类二次根式即可;
(2)利用平方差公式计算;
(3)根据二次根式的乘除法则运算;
(4)根据负整数指数的意义和二次根式的除法法则运算;
(5)先把分数指数的形式化为二次根式的形式,然后化简后合并即可.
解答 解:(1)原式=$\frac{13\sqrt{5}}{4}$;
(2)原式=[(2$\sqrt{3}$+3$\sqrt{2}$)(2$\sqrt{3}$-3$\sqrt{2}$)]2
=(12-18)2
=36;
(3)原式=$\frac{5}{6}$×6×$\frac{3}{2}$×$\frac{1}{5}$×$\sqrt{10×7×\frac{1}{10}×7}$
=$\frac{3}{2}$×7
=$\frac{21}{2}$;
(4)原式=$\sqrt{2}$-1+2$\sqrt{6÷3}$
=$\sqrt{2}$-1+2$\sqrt{2}$
=3$\sqrt{2}$-1;
(5)原式=2$\sqrt{5}$-3$\sqrt{5}$+$\sqrt{8}$×$\sqrt{2}$+$\frac{3}{4}$-$\frac{3}{2}$
=-$\sqrt{5}$+4-$\frac{3}{4}$
=$\frac{13}{4}$-$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
1.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如表:
经检查,发现表格中恰好有一组数据计算错误,错误的那组数据的序号是( )
| 序号 | ① | ② | ③ | ④ | ⑤ |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 8 | 3 | 0 | 1 | 0 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
19. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )| A. | $\frac{π+\sqrt{2}-1}{2}$cm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D. | $\frac{π+\sqrt{3}-1}{2}$cm2 |
20.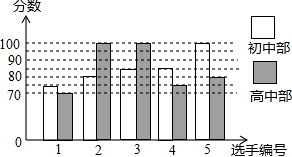 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
求得初中代表队选手决赛成绩的平均数和方差:
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85,
${{S}_{1}}^{2}$=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70;
(1)根据图示填写表格:
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.求得初中代表队选手决赛成绩的平均数和方差:
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85,
${{S}_{1}}^{2}$=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70;
(1)根据图示填写表格:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
(3)计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
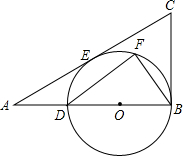 如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.
如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.