Question

8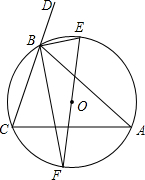．如图，已知BF、BE分别是△ABC的内角∠ABC与外角∠ABD的平分线，BF、BE分别与△ABC的外接圆O交于点F、E．求证：
（1）EF是△ABC的外接圆的直径；
（2）EF是AC的垂直平分线．

Answer 1

分析 （1）根据角平分线的定义求出∠EBF=90°，根据圆周角定理证明结论；
（2）根据垂径定理及其推论证明即可．

解答 证明：（1）∵BF、BE分别是△ABC的内角∠ABC与外角∠ABD的平分线，
∴∠EBA=$\frac{1}{2}$∠DBA，∠FBA=$\frac{1}{2}$∠CBA，
∴∠EBA+∠FBA=$\frac{1}{2}$（∠DBA+∠DBA）=90°，
即∠EBF=90°，
∴EF是△ABC的外接圆的直径；
（2）∵BF是∠ABD的平分线，
∴∠CBF=∠ABF，
∴$\widehat{CF}$=$\widehat{AF}$，又EF是△ABC的外接圆的直径，
∴EF是AC的垂直平分线．

点评 本题考查的是三角形的外接圆和外心的概念及其性质、垂径定理及其推论，掌握90°的圆周角所对的弦是直径和过圆心平分弧则垂直平分弦是解题的关键．