题目内容
16.$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\frac{1×(\sqrt{5}-\sqrt{4)}}{(\sqrt{5}+\sqrt{4})(\sqrt{5-\sqrt{4})}}$=$\frac{\sqrt{5}-\sqrt{4}}{{(\sqrt{5})}^{2}{-(\sqrt{4})}^{2}}$=$\sqrt{5}$$-\sqrt{4}$=$\sqrt{5}$-2$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\frac{1×(\sqrt{6}-\sqrt{5)}}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}$=$\frac{\sqrt{6}-\sqrt{5}}{{(\sqrt{6})}^{2}{-(\sqrt{5})}^{2}}$=$\sqrt{6}$-$\sqrt{5}$
请回答下列问题:
(1)观察上面的解题过程.请直接写出结果.$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$
(2)利用上面提供的信息请化简:
$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2007}+\sqrt{2008}}$的值.
分析 (1)利用已知数据变化规律直接得出答案;
(2)利用分母有理化的规律将原式化简进而求出即可.
解答 解:(1)$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\frac{\sqrt{n}-\sqrt{n-1}}{(\sqrt{n}+\sqrt{n-1})(\sqrt{n}-\sqrt{n-1})}$=$\sqrt{n}$-$\sqrt{n-1}$;
故答案为:$\sqrt{n}$-$\sqrt{n-1}$;
(2)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2007}+\sqrt{2008}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2008}$-$\sqrt{2007}$
=$\sqrt{2008}$-1
=2$\sqrt{502}$-1.
点评 此题主要考查了分母有理化,正确化简二次根式是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
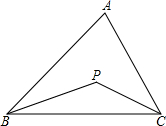 如图,△ABC的两内角平分线交于点P.
如图,△ABC的两内角平分线交于点P.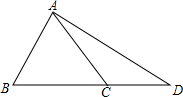 如图,C是△ABD的边BD上的一点,且AC=BC,你能判断AD与BD的大小吗?
如图,C是△ABD的边BD上的一点,且AC=BC,你能判断AD与BD的大小吗?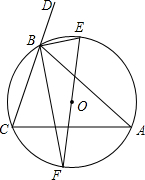 如图,已知BF、BE分别是△ABC的内角∠ABC与外角∠ABD的平分线,BF、BE分别与△ABC的外接圆O交于点F、E.求证:
如图,已知BF、BE分别是△ABC的内角∠ABC与外角∠ABD的平分线,BF、BE分别与△ABC的外接圆O交于点F、E.求证: 已知:如图,在四边形ABCD中,AB=CD,∠BAC=∠ACD,求证:△ABC≌△CDA.
已知:如图,在四边形ABCD中,AB=CD,∠BAC=∠ACD,求证:△ABC≌△CDA.